tp-le-systeme-solaire-et-l-annee-de-lu

THEME L’UNIVERS
PARTIE 1 PRESENTATION DE L’UNIVERS
TP U1 : LE SYSTEME SOLAIRE ET LES DIMENSIONS DES OBJETS DANS
L’UNIVERS
OBJECTIFS :
 Utiliser l’écriture scientifique pour classer et comparer les dimensions
 Comprendre la notion d’années de lumière
 Expliquer l’expression : « voir loin, c’est voir dans le passé »
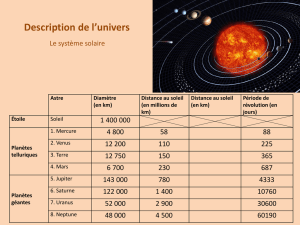
I. DIMENSIONS DANS LE SYSTEME SOLAIRE
1. Manipulation
Ouvrir le logiciel Winstars 2 (logiciel gratuit téléchargeable sur le site www.winstars.net)
Dans le menu Options, sélectionner Configuration générale > Planètes et cocher l’affichage des noms des planètes et des
orbites.
Dans le menu Observations, cliquer sur Voir le Système Solaire en entier
À l’aide des outils dédiés, zoomer et centrer la fenêtre sur le Soleil afin de visualiser l’orbite et les positions de Vénus, la
Terre et Mars
 Pour chacune des 3 planètes, mesurer en cm la valeur à l’écran du diamètre moyen de son orbite. En déduire la valeur
à l’écran de son rayon, lequel représente la valeur moyenne de la distance entre la planète et le Soleil.
 Agir sur le zoom pour faire apparaître Jupiter. L’échelle ayant changé, déterminer de nouveau en cm la valeur à
l’écran du rayon de l’orbite de Mars. Faire la mesure pour Jupiter.
 Agir de nouveau sur le zoom pour faire apparaître Uranus. Effectuer la mesure à l’écran du rayon de l’orbite de
Jupiter, Saturne et Uranus.
 Agir une dernière fois sur le zoom pour faire apparaître Neptune. Terminer par la mesure à l’écran du rayon de
l’orbite d’Uranus et de Neptune.
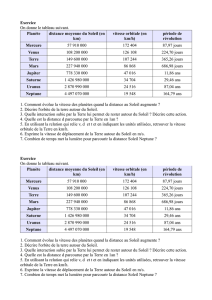
2. Exploitation
1) Calculez le rapport des distances au Soleil de Vénus et Mars sur la distance Soleil-Terre.
2) Calculez le rapport de la distance au Soleil de Jupiter sur la distance Soleil-Mars. Déduisez-en le rapport de la distance
Soleil-Jupiter sur la distance Soleil-Terre.
3) Procédez de même pour déterminer le rapport des distances au Soleil de Saturne, Uranus et enfin Neptune, sur la
distance Soleil-Terre.
4) L’unité astronomique (notée ua) est égale à la distance Soleil-Terre. Regrouper dans la première ligne du tableau les
distances en ua séparant le Soleil de chacune des planètes du système solaire. La distance Soleil-Mercure est égale à
0,38 ua.
Astre
Mercure
Venus
Terre
Mars
Jupiter
Saturne
Uranus
Neptune
Distance
Soleil-astre
en u.a.
Distance
Soleil-astre
en USI
5) Graduer un axe en unité astronomique u.a et y placer les planètes du système solaire, en prenant pour origine le soleil

6) La distance Terre –Soleil vaut DT-S = 150.106 km. Exprimer cette distance en écriture scientifique et en unité du
système international (USI)
7) En déduire la valeur d’1 u.a. en USI
8) Exprimer les distances précédentes en USI, puis les regrouper dans la deuxième ligne du tableau
II. VOIR LOIN, C’EST VOIR DANS LE PASSE
1. Document
En 1676, le Danois Olaus Römer comprit le premier que la vitesse de la lumière n’était pas infinie. L’étude et la connaissance
de l’Univers lointain en furent bouleversées.
« C’est à la fin du XXème siècle que de grands télescopes ont été construits pour sonder l’Univers jusque dans ses confins
reculés. Ainsi, le télescope spatial Hubble met à profit sa position privilégiée dans le vide interplanétaire pour scruter les
galaxies jusqu’aux distances les plus impressionnantes. Il est important de comprendre que, à l’échelle des longueurs qui
séparent les galaxies, la lumière met du temps pour parcourir ces espaces immenses. Si rapide soit-elle (sa vitesse atteint
300 000 kilomètres par seconde), il lui faut ainsi de nombreuses années pour parvenir jusqu’à nous depuis les corps célestes
qui peuplent l’Univers : dix années pour l’étoile la plus proche, Proxima Centauri, et deux millions d’années pour la galaxie
d’Andromède, pourtant encore visible à l’œil nu !
Les astronomes expriment les longueurs cosmiques grâce à l’année de lumière (notée al), qui désigne la distance parcourue
par la lumière en une année. La galaxie d’Andromède se trouve donc à la distance de deux millions d’années de lumière. Mais
cela signifie aussi que, lorsque nous la contemplons, la lumière qui nous la montre l’a quittée il y a deux millions d’années.
Autrement dit, nous la voyons telle qu’elle était il y a deux millions d’années.
Observer l’Univers lointain, c’est le voir dans le passé. »
D’après A. Dollfus, Les autres mondes, Belin, 2008.
2. Exploitation
1) Exprimez la valeur de la vitesse c de la lumière en m/s. Indiquez le résultat en notation scientifique avec 3 chiffres
significatifs.
2) Quelle est, en seconde, la durée d’une heure ? d’un jour ? d’une année de 365 jours ?
3) Quelle est la définition de l’année de lumière (al) donnée dans le document ?
4) La distance parcourue par la lumière pendant la durée ∆T étant égale à c∆T, calculez en mètre la valeur de l’année de
lumière.
5) Calculer la distance en km nous séparant de la galaxie d’Andromède
6) En supposant que la technologie permette un jour de se déplacer à la vitesse de la lumière, combien faudrait-il de temps
pour atteindre Proxima Centauri ? La Galaxie d’Andromède ? Commenter
7) La galaxie M 81 est située à 11,8 millions d’al de la Terre. L’âge des ossements de l’hominidé Toumaï, exhumés en 2001
au Tchad, en Afrique, a été évalué à 7 millions d’années. Toumaï était-il né au moment où la lumière qui nous parvient
aujourd’hui de M 81 a quitté cette galaxie ?