corrigé du DM de 4ème de décembre

Mathématiques Classe de 4ème
Mathématiques Classe de 4ème
D
DE EV VO OI IR R M MA AI IS SO ON N
de décembre 2010
de décembre 2010
corrigé réalisé à partir des travaux de plusieurs élèves de 4A et 4E
corrigé réalisé à partir des travaux de plusieurs élèves de 4A et 4E
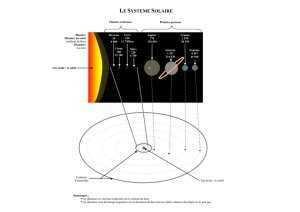
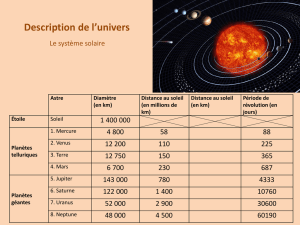
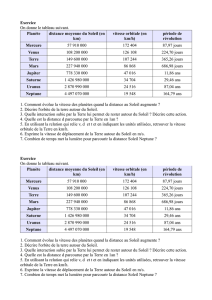
Exercice : les planètes du système solaire.
1) Dans le tableau ci-dessous figurent toutes les planètes du système
solaire ainsi que des valeurs approchées de leurs distances moyennes au
Soleil :
Planètes Distances au Soleil en millions de
km
Distances en u.a.
Mercure 57,9 0,38
Vénus 108,2 0,72
Terre 149,6 1
Mars 227,6 1,52
Jupiter 778,3 5,21
Saturne 1427 9,52
Uranus 2869 19,16
Neptune 4505 30,11
Ainsi, une unité astronomique (1 u.a.) est égale à la distance de la Terre au Soleil.
2. La loi de Titius-Bode.
La loi de Titius-Bode permet de calculer de façon approximative les distances des planètes au Soleil exprimées
en unités astronomiques, grâce à la formule : Distance = 0,4 + 0,3 × 2n où n est un entier.
Pour n=-1; D=0,4+0,3x 2-1 = 0,5 -1 est associé avec Mercure.
Pour n=0 ; D=0,4+0,3x 20 = 0,7 0 est associé avec Vénus.
Pour n=1 ; D=0,4+0,3x 21 = 1 1 est associé avec la Terre.
Pour n=2 ; D=0,4+0,3x 22 = 1,6 2 est associé avec Mars.
Pour n=3 ; D=0,4+0,3x 23 = 2,8
Pour n=4 ; D=0,4+0,3x 24 = 5,2 4 est associé avec Jupiter.
Pour n=5 ; D=0,4+0,3x 25 = 10 5 est associé avec Saturne.
Pour n=6 ; D=0,4+0,3x 26 = 19,6 6 est associé avec Uranus.
Pour n=7 ; D=0,4+0,3x 27 = 38,8 7 est associé avec Neptune
Il y a deux planètes pour lesquelles l'écart avec la distance prévue par la loi de Titius-Bode est assez
important. Ces deux planètes sont Neptune et Saturne. Il semble qu'avec cette loi, il y ait un « trou », par la
valeur n = 3. Ce « trou » correspond à la ceinture d’astéroïde entre Mars et Jupiter.

Le défi du mois : les losanges
On peut compter 16 petits losanges et le grand donc 17.
On peut ensuite compter 9 autres losanges (de taille 2 sur 2) .
On peut aussi compter les 4 losanges de 3 carreaux de côté.
Avec le grand losange (de taille 4 sur 4) on obtient un total de
16 + 9 + 4 + 1 = 4² + 3² + 2² + 1² = 30
Il y a en tout 30 losanges.