Ch 4 Triangles et parallèles

CHAPITRE 4 TRIANGLES ET PARALLELES
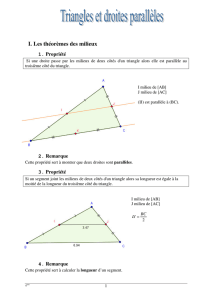
I Propriétés relatives aux milieux de deux côtés d’un triangle.
Si I milieu de [AB] et J milieu de [AC] alors (IJ) est parallèle à (BC)
Si I milieu de [AB] et (IJ) est parallèle à (BC) alors J milieu de [AC]
Si I milieu de [AB] et J milieu de [AC] alors  =
1) Propriété des milieux :
Si une droite passe par les milieux de deux côtés d’un triangle, alors
elle est parallèle au troisième côté.
2) Réciproque :
Si une droite passe par le milieu d’un côté d’un triangle et est parallèle à un deuxième
côté de ce triangle, alors elle coupe le troisième côté en son milieu.
3) Si, dans un triangle, un segment joint les milieux de deux côtés alors sa longueur est égale à la
moitié de celle du troisième côté.

II Droite parallèle à un côté d’un triangle.
Petit théorème de Thalès:
Si, dans un triangle ABC, M est un point de [AB], N un point de [AC] et si la droite (MN) est
parallèle au côté [BC] alors
BC
MN
AC
AN
AB
AM ==
Exemple : Dans le triangle DST, E est un point de [DS] et F un point de [DT] tels que DS =
6,3cm ;
EF = 2,9 cm ; ST = 8,7 cm et DF = 1,8 cm. Les droites (EF) et (ST) sont parallèles. Calculer DE et
DT.
La figure n’est pas à l’échelle
E est un point de [DS], F un point de [DT], et les droites (EF)
et (ST) sont parallèles.
On a donc
ST
EF
DT
DF
DS
DE
==
soit 7,8 9,28,1
3,6 == DT
DE
7,8 9,2 3,6 =
DE 7,8 9,28,1 =
DT
7,8 3,69,2
×
=DE 9,2 7,88,1
×
=DT
cmDE 1,2
=
cmDT 4,5
=
S
T
D
E F

III Agrandissement, réduction
Quand deux figures ont la même forme et des longueurs proportionnelles, on dit que l’une est
l’agrandissement ou la réduction de l’autre.
Le coefficient de proportionnalité est le rapport d’agrandissement ou de réduction.
Dans un agrandissement ou une réduction, les mesures des angles, la perpendicularité et le
parallélisme sont conservés.
Exemples :
• Le triangle BEC est une réduction de rapport
4
3 du triangle TOP de côtés 3,6 cm, 5,2 cm
et 7,2 cm. Construire le triangle BEC.
Comme BEC est une réduction de TOP de rapport
4
3 alors ses dimensions sont
4
3 de fois celles
du triangle TOP.
4
3× 3,6 = 2,7
4
3× 5,2 = 3,9
4
3× 7,2 = 5,4
Les longueurs du triangle BEF sont 2,7 cm, 3,9 cm et 5,4 cm.
• Le triangle PAS est tel que APS = 100°, SAP = 50° et PA = 3 cm. PIN est un
agrandissement du triangle PAS de rapport 2,5. Construire le triangle PIN.
Comme PIN est un agrandissement de PAS de rapport 2,5 alors ses dimensions sont multipliées
par 2,5 donc PI (ou PN) = 2,5×3 soit 7,5 cm.
Par contre, les mesures des angles sont conservés donc PIN = 50° (ou PNI) et IPN = 100° (ou NPI).