T1 : Mouvement de rotation

P CORMERAIS Mouvement de rotation P CORMERAIS
Page 1 sur 3
T 1
2 BAC PROFESSIONNELLE
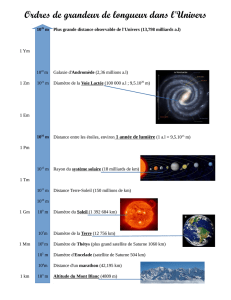
COMMENT PASSER DE LA VITESSE DES ROUES
Á CELLE DE LA VOITURE ?
I LE MOUVEMENT DE ROTATION
Quelle trajectoire décrivent les points M ?
II FREQUENCE DE ROTATION
Pour un objet tournant autour d'un axe, on peut définir la fréquence de rotation n:
Le compte-tours d'une voiture indique une fréquence de rotation
que l'on notera N en tours par minute.
III VITESSE LINEAIRE ET FREQUENCE DE ROTATION
La vitesse d'avancement d'une voiture dépend de la fréquence
de rotation de ses roues et de leur rayon:
2R
En un tour, la roue avance d'une longueur égale à son périmètre: 2R
Avec une fréquence de rotation n, le déplacement est 2R.n en une seconde, d'où la vitesse linéaire v
du véhicule :
v en m/s (mètre par seconde)
N =
La fréquence de rotation n s'exprime en ....................... par
seconde (tr/s) et désigne le nombre de tours effectués en
une seconde par l'objet en rotation.
Un solide est en mouvement de rotation autour d’un axe si tous les points autres que l’axe
décrivent un ............................
v =...........................

P CORMERAIS Mouvement de rotation P CORMERAIS
Page 2 sur 3
IV APPLICATIONS TECHNOLOGIQUES
1° Transmission par courroie ou poulie
Relation liant les fréquences de rotation et les diamètres
2° Réducteur à engrenages
Relation liant les fréquences de rotation
et le nombre de dents des pignons
V EXERCICES
1° Calculer la fréquence de rotation de l'aiguille des secondes d'une montre.
2° Déterminer la fréquence de rotation de la Terre autour de son axe en admettant que la Terre effectue un
tour en 24 heures.
En déduire la vitesse d'un point situé à l'équateur si la circonférence de la Terre mesure 40000 km.
3° Une meule à tronçonner travaille à une vitesse périphérique de 20 m/s. En déduire la fréquence de
rotation de la meule lorsqu'elle a un diamètre de 40 mm..
4° On définit pour toute automobile :
* Le rapport de démultiplication d de la boite de vitesse ;
* Le rapport de transmission t entre la boite et l'axe des roues.
On considère une automobile dont le rapport de démultiplication d en 4ème est 1,2 (le pignon de la boite de
vitesse tourne 1,2 fois moins vite que l'axe moteur) et dont le rapport de transmission t est 3,5 (le pignon de
la boite de vitesse tourne 3,5 fois plus vite que l'axe des roues. Le diamètre des roues est de 52 cm.
Quel doit être en tr/min, le régime du moteur pour qu'en 4 ème la vitesse de la voiture soit de 100 km/h ?
a) Convertir la vitesse en m/s
b) Calculer la fréquence de rotation des roues en tr/s
c) En déduire la fréquence de rotation de l’axe de transmission puis du moteur
d) Calculer la fréquence de rotation du moteur en tr/min
5° Le système d'engrenage suivant comporte 3 roue de nombres de dents suivants :
Z1 = 40 dents Z2 = 20 dents Z3 = 10 dents.
a) Déterminer le sens de rotation de la roue 3
b) La roue 1 tourne à 1500 tours / min, calculer les fréquences de
rotation des 2 autres roues. 1 2 3
c) Le diamètre de la roue 1 est 12 cm, calculer le diamètre et la vitesse linéaire des autres roues.
6° Un moteur électrique tournant à 1500 tr/min doit entraîner une machine par courroie à la vitesse
de 600 tr/min. Sachant que la poulie calée sur le moteur a un diamètre de Dl = 200 mm, calculer le diamètre
D2 de la poulie de la machine et la vitesse de d’un point de la courroie.

P CORMERAIS Mouvement de rotation P CORMERAIS
Page 3 sur 3
7° Un foret de 12 mm de diamètre tourne à 300 tours / min.
Calculer la vitesse linéaire d'un point de sa périphérie.
8° Un outil circulaire, de diamètre 140 mm, tourne à la fréquence de rotation constante de 7 500 tr/min.
a) Calculer sa fréquence de rotation.
b) Déterminer la vitesse d'usinage, c'est à dire la vitesse linéaire d'un point de la circonférence de l'outil.
9° L’arbre d'un moteur est directement accouplé à l'axe de la roue entraînant un tapis roulant. Le diamètre de
la roue est 1,20 m. Quelle doit être la fréquence de rotation du moteur pour qu'un objet situé sur le tapis
avance avec une vitesse constante de 100 m/min ?
10° Soit le réducteur de vitesse schématisé ci-dessous ; il est
constitué de 2 poulies de diamètres différents reliées par une
courroie rigide. La poulie (1) tourne à une fréquence de
rotation n1 = 1 100 tr/min ; son diamètre D1 = 5 cm.
a )En déduire la vitesse linéaire d'un point de la courroie M1.
b) Quelle est la vitesse linéaire d'un point de la courroie M2 ?
c) En déduire la fréquence de rotation n2 de la poulie 2 sachant
que son diamètre D2 = 22 cm.
d) Quel diamètre faut il choisir pour la poulie 2 si l'on veut
qu'elle tourne à 700 tr/min ?
11° Le fabricant d’une ponceuse indique :
a) Convertir le diamètre D de la meule en mètre.
b) Convertir la fréquence n en tour par seconde.
c) À l'aide de la formule v = π D n , calculer, arrondie au m/s, la
vitesse v d'un point situé sur la circonférence de la meule quand celle-
ci tourne à la fréquence de 183,3 tr/s.
d) Convertir cette vitesse en km/h.
12° Une charge est levée par à un treuil entraîné par un moteur.
Le treuil a un diamètre de 19 cm et achemine la charge à une hauteur de 6 m.
a) Calculer le nombre de tours nécessaires pour élever cette charge.
Arrondir le résultat à l'unité.
b) La fréquence de rotation du treuil est de 20 tr/min, calculer la durée
nécessaire pour élever
13°Une partie de la chaîne d’étiquetage des bouteilles de champagne est représentée par le schéma ci-dessous.
Lorsque le carrousel effectue un tour complet, il capte 12 bouteilles.
a) Ce carrousel permet l’étiquetage de 3 240 bouteilles à l’heure.
Calculer la fréquence de rotation en tr/min du carrousel. En déduire sa vitesse angulaire arrondie à 0,001 rad/s.
b) Calculer la vitesse de déplacement d’une bouteille, arrondie à 0,001 m/s. La fréquence du carrousel de diamètre
60 cm de rotation est 0,075 tr/s. (Diamètre du carrousel : 60 cm).