13 Axes de symétrie

CH XII AXES de symétrie d'une figure
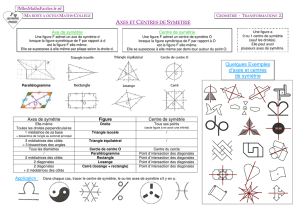
1. Définition
Un axe de symétrie d'une figure est une droite qui partage cette figure en deux parties
superposables par pliage le long de cette droite.
Combien d'axes de symétrie ?
0 1 2 3 4 5
2. Axe de symétrie d'un segment
A) Utilisation d'un calque
La médiatrice d'un segment est son axe de symétrie.
Les points A et B sont symétriques par rapport à la droite d.
Le point M est à égal distance de A et de B. ( MA = MB)
B) Construction au compas
d
♘
☐
⚁
♙
//
//

3. Axe de symétrie d'un angle
J'utilise un calque
J'utilise le compas
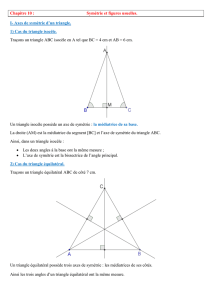
4. Axe de symétrie d'un triangle
Construire un triangle ABC avec la droite d comme axe de symétrie ?
• Deux sommets sont symétriques (A et B par exemple)
• Le troisième sommet C est sur l'axe de symétrie
Le triangle ABC est isocèle
Je retiens
Un triangle isocèle est un triangle qui a un axe de symétrie.
Les angles à la base sont égaux.
Un triangle équilatéral est un triangle qui a 3 axes de symétrie.
Les trois angles sont égaux.
Bissectrice
Arc de cercle de centre H
Arc de cercle de centre I
de même rayon
d
//
//

5. Axe de symétrie d'un quadrilatère
Activité
Placer quatre points pour que la droite d soit un axe de symétrie du quadrilatère ABCD.
•!On place le premier sommet A.
• Le deuxième sommet B est symétrique de A.
• On place le troisième sommet C.
• Le quatrième sommet D est symétrique de C
On obtient :
[AB] // [CD]
AC = BD
C'est un trapèze isocèle.
•!On place le premier sommet A.
• Le deuxième sommet B est symétrique de A.
• On place le troisième sommet C sur l'axe de symétrie
• Le quatrième sommet D est aussi sur l'axe de symétrie.
On obtient :
DA = DB
CA = CB
C'est un cerf-volant.
6. Rectangle. Losange et carré
Rectangle
Deux axes de symétrie : d1 et d2
[OA] et [OB] sont symétriques / d1 donc :
OA = OB
[OB] et [OC] sont symétriques / d2 donc :
OB = OC
[OC] et [OD] sont symétriques / d1 donc
OC = OD
Donc OA = OB = OC = OD
Je retiens :
Dans un rectangle, les diagonales sont égales et se coupent en leur milieu.
//
//
d
//
//
/
/
d1
d2
O
//
//
//
//

Carré
Quatre axes de symétrie : d1, d2, d3 et d4.
Je retiens :
Sans un carré, les diagonales sont égales,
se coupent en leur milieu et sont perpendiculaires.
Losange
Deux axes de symétrie : les deux diagonales.
Je retiens :
Dans un losange, les diagonales sont perpendiculaires,
se coupent en leur milieu.
Dans un losange, les angles sont égaux 2 à 2.
d3
d2
d1
d4
//
//
// //
//
//
/
/