Dossier - Infomars

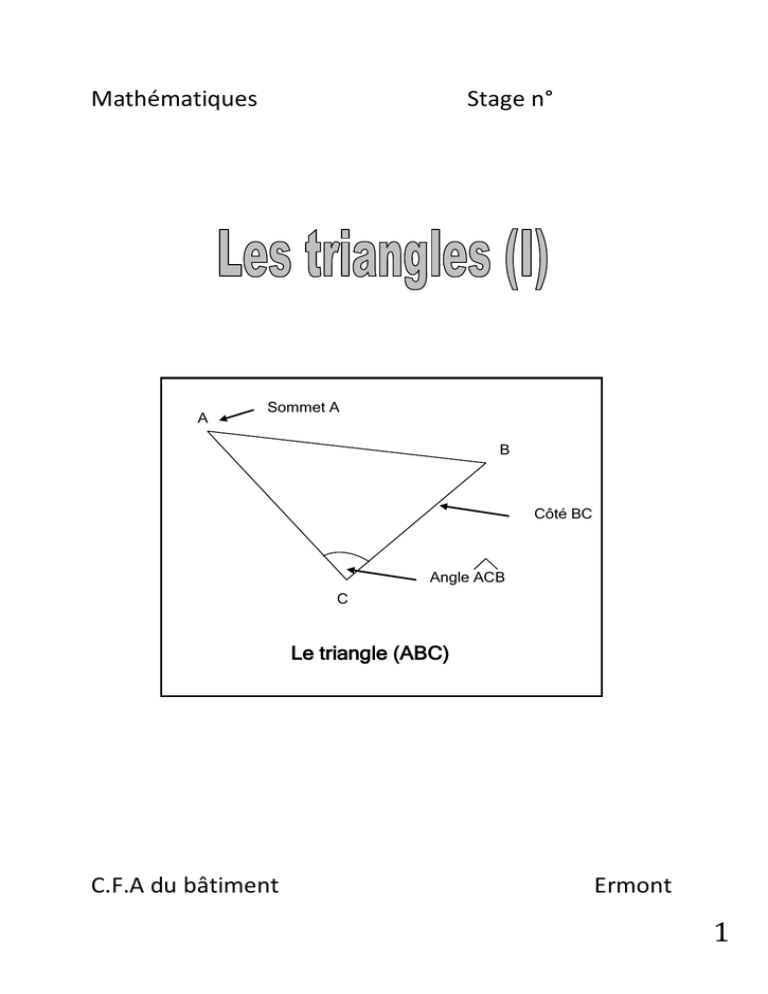
Mathématiques
A
Stage n°
Sommet A
B
Côté BC
Angle ACB
C
Le triangle (ABC)
C.F.A du bâtiment
Ermont
1
Rappel de quelques évidences :
Un triangle est une forme géométrique fermée à 3 côtés. Il a également 3 sommets, ainsi
que 3 angles.
Problème :
La figure ci-dessous permet de se persuader que la somme des 3 angles d’un triangle fait
toujours 180 °. Avez-vous trouvé comment faire ?
En conclusion :
………………………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………………………
2
Les triangles particuliers
Certains triangles peuvent avoir une ou plusieurs particularités :
Avoir deux ou trois côtés égaux.
Avoir un angle droit.
Si ce n’est pas le cas, on dit que le triangle est quelconque.
Faisons le point sur les triangles particuliers qui peuvent exister.
Le triangle ____________________________
Il a 2 côtés égaux.
Sur le dessin, indiquez que deux côtés ont la même longueur
avec un symbole approprié.
Que peut-on dire de ses angles ?
Le triangle ____________________________
Il a 3 côtés égaux.
C’est en quelque sorte le triangle « parfait ».
Sur le dessin, indiquez que ses trois côtés ont la même longueur
avec un symbole approprié.
Que peut-on dire de ses angles ?
Le triangle ____________________________
Un de ses angles est un angle droit (90°)
Sur le dessin, indiquez la présence de l’angle droit avec le
symbole approprié.
3
Exercice 1 :
Quelle est la nature de ce triangle ? Pourquoi ?
Exercice 2 :
Quelle est la nature de ce triangle ? Pourquoi ?
Exercice 3 :
Quelle est la nature de ce triangle ? Pourquoi ?
Exercice 4 :
Quelle est la nature de ce triangle ? Pourquoi ?
74°
32°
Exercice 5 :
Calculez la valeur de l’angle ABC. Justifiez votre
réponse.
60°
Exercice 6 :
Calculez la valeur de l’angle EFG. Justifiez votre
réponse.
63°
84°
Exercice 7 :
Le triangle (ABC) est-il rectangle ? Justifiez votre
réponse.
32°
86°
4
Exercice : un triangle particulier particulier …
1) Tracez un triangle (FGH) tel que :
Un angle droit se trouve en G
FG = GH = 6cm
2) Quelles sont les particularités de ce triangle ? Comment pourrait-on l’appeler ?
3) Que peut-on dire de ses deux angles non droits ?
4) Calculez ces deux angles.
5
Problème :
1) Tracez un quadrilatère quelconque (ABCD) , un carré (EFGH) et un rectangle (IJKL).
2) Calculez la somme des angles de (EFGH) et de (IJKL)
3) On voudrait désormais connaître la somme des angles de (ABCD) : sauriez vous
démontrer que cette somme vaut 360 ° ?
(Astuce : et si vous traciez une diagonale à ce quadrilatère …)
4) A main levée, schématisez un pentagone régulier et un hexagone régulier (ils ont
respectivement 5 et 6 côtés).
5) Sauriez vous trouvez une méthode pour calculer la somme de leurs angles ?
6
Synthèse
Les triangles quelconques
Leurs 3 côtés ont des longueurs différentes
Leurs 3 angles ont des valeurs différentes
Mais la somme des 3 angles fait toujours 180°
Les triangles particuliers
Le triangle isocèle
Il a 2 côtés égaux et aussi 2 angles égaux.
Le triangle équilatéral
Il a 3 côtés égaux, et ses 3 angles valent 60°.
Le triangle rectangle
Il possède un angle droit (= 90°)
Mais la somme des 3 angles fait toujours 180°
7