CALCULATRICE AUTORISEE SAUF InSPIRE

DS5 – Bac Blanc n°1 – Lycée Montaigne – Février 2017 Page 1
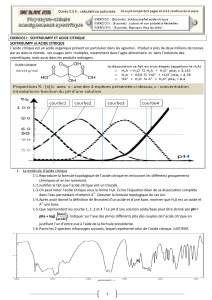
1. L’acide citrique.
1. A partir de la formule semi-développée de l’acide citrique donnée ci-dessus, établir la formule topologique de l’acide
citrique.
2. Entourer sur cette formule, les différents groupements chimiques (si vous n’êtes pas sûr de votre réponse
précédente, reproduire alors la formule semi-développée donnée ci-dessus et répondre à l’aide de cette
représentation à la question).
Nommer les groupes et préciser la famille correspondante.
3. L’acide citrique possède des propriétés acidobasiques en solution aqueuse. Justifier le fait que l’acide citrique soit
un triacide.
4. L’acide citrique étant un triacide, il est noté H3A(Aq). Ecrire l’équation-bilan de sa dissociation complète dans l’eau
permettant d’obtenir A3-(Aq).
5. Dessiner la formule topologique de cet ion.
6. Après avoir donné la définition d’un acide et d’une base, montrer que H3A(Aq) est un acide et que A3-(Aq) est la base
associée.
BACCALAURÉAT GÉNÉRAL Session Janvier 2017
PHYSIQUE-CHIMIE Série S
Durée de l’épreuve : 3 heures 30
Lycée Michel de Montaigne
CALCULATRICE AUTORISEE SAUF InSPIRE
Exercice I (9 points)
L’acide citrique est un acide organique présent en particulier dans les agrumes.
Produit à près de deux millions de
tonnes par an dans le monde, ses usages sont multiples, notamment dans l’agro-alimentaire et dans l’industrie des
cosmétiques, mais aussi dans les produits ménagers.
L’acide citrique a pour formule semi-développée :
Masse molaire : M = 192 g.mol1
HOOC
CH
2
OH
COOH
COOH
CH
2
C

DS5 – Bac Blanc n°1 – Lycée Montaigne – Février 2017 Page 2
7. Que représentent les courbes 1, 2, 3 et 4 ? Associer à chaque courbe une espèce chimique.
8. Le pH d’une solution acide/base peut être donnée par
 Acide
Base
pKpH alog .
Indiquer sur l’axe des pH DE LA FIGURE 1 DE L’ANNEXE A RENDRE AVEC LA COPIE, les
différents pKa des couples de l’acide citrique en justifiant l’un d’entre eux à l’aide de la formule précédente.
9. Parmi les deux spectres IR proposés ci-dessous, lequel représente celui de l’acide citrique. Justifier la réponse.
10. Montrer que le spectre RMN donné ci-dessous ne peut pas être celui de l’acide citrique. Justifier votre réponse par
un raisonnement construit.
Spectre IR n°1.
Spectre IR n°2
Document
Spectre RMN.

DS5 – Bac Blanc n°1 – Lycée Montaigne – Février 2017 Page 3
2. Dosage de l’acide citrique.
11. Trouver la valeur du pH à l’équivalence. Vous ferez apparaître la méthode sur LA FIGURE 2 DE L’ANNEXE A
RENDRE AVEC LA COPIE.
Montrer que pour ce pH l’ion A3-(Aq) est majoritaire.
12. Résolution de problème.
Par un raisonnement détaillé, déterminer la masse d’acide citrique contenue dans le bonbon.
P
rotocole
Dissoudre un bonbon dans 50 mL d’eau. On obtient une solution S.
Doser 10 mL de la solution S par de l’hydroxyde de sodium (Na+(Aq), HO-(Aq)) de concentration Cb = 0,08 mol.L-1.
Le suivi pH métrique donne la courbe ci-dessous.
L’équation de la réaction, support du titrage, est la suivante : )(2
3
)(3 033 )()( LiqAq HAHOAH AqAq  

DS5 – Bac Blanc n°1 – Lycée Montaigne – Février 2017 Page 4
Exercice II (6 points)
1. La poussée de la fléchette.
1. Donner l’expression vectorielle de la quantité de mouvement p du système {fléchette – pistolet}, en fonction des
données de l’exercice, avant que Ludovic ne déclenche le tir. En déduire sa valeur.
2. Donner l’expression vectorielle de la quantité de mouvement 'p du système {fléchette – pistolet}, en fonction des
données de l’exercice, à la fin de la phase de poussée.
3. Quelle relation peut-on établir entre ces deux quantités de mouvement ? Justifier votre réponse.
4. En déduire la valeur vP de la vitesse de recul du pistolet juste après l’éjection de la fléchette.
5. La valeur réelle de cette vitesse est beaucoup plus faible que la valeur que l’on obtient à la question précédente.
Pourquoi observe-t-on une telle différence ?
6. Donner la direction, le sens et la valeur du vecteur accélération de la fléchette. Justifier vos réponses.
7. Quelles sont les deux forces s’exerçant sur la fléchette au cours de la phase de poussée ? Quelle condition doivent
vérifier ces deux forces pour que la fléchette démarre son mouvement ?
8. En appliquant la seconde loi de Newton, déterminer la valeur de la force de poussée exercée par le pistolet sur la
fléchette.
2. La montée de la fléchette.
9. Quelle est la représentation cohérente avec la situation donnée ? Une justification précise est attendue.
Ludovic décide d’utiliser ses connaissances en mécanique pour étudier le mouvement
d’une flèche tirée par son pistolet.
Il néglige toute action de l’air et prend g = 10 m.s-2 pour valeur de la constante de
pesanteur.
Il considère la fléchette comme un objet ponctuel de masse m1 = 50g.
L’étude se décompose en deux parties :
 Une première correspond à la poussée de la fléchette par le pistolet
 La seconde s’intéressant à la monte verticale de la fléchette, une fois
éjectée du pistolet.
On considère que le système {fléchette
–
pistolet} est un système isolé. La masse du pistolet à vide
est m
P
= 115g.
Au cours de cette phase de poussée, d’une durée st 30,0
0 , la fléchette passe de l’immobilité à la vitesse verticale
v
1
= 4,5 m.s
-1
.
La fléchette est maintenant
libérée du pistolet avec une vitesse v
1
= 4,5 m.s
-
1
au point O du schéma avec Ludovic, et évolue
librement vers le haut. On peut montrer que lors de cette montée , la vitesse vy de la fléchette selon l’axe vertical y, vérifie
la relation vy= - 10 x t + 4,5
Les représentations graphiques données ci-dessous, proposent 4 évolutions au courant du temps de la vitesse vy de la
fléchette suivant l’axe vertical.

DS5 – Bac Blanc n°1 – Lycée Montaigne – Février 2017 Page 5
Exercice III OBLIGATOIRE (5 points)