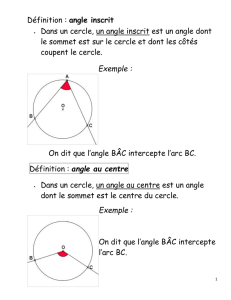
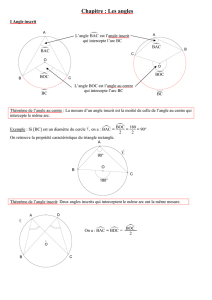
Chapitre 3 : Angles inscrit et au centre dans un cercle

Chapitre 3 : Angles inscrit et au centre dans un cercle
1. Problème
Hypothèses :
•ABC est un triangle isocèle.
•E est le symétrique de B par rapport à A.
L'armation suivante est-elle vraie ?
Armation : Pour n'importe quelle valeur de
̂
ABC
, on a :
̂
EAC=2
̂
ABC
2. Conjecture
Hypothèses :
•ABC est un triangle isocèle.
•E est le symétrique de B par rapport à A.
Conjecture : Il semble que l'armation soit vraie.

3. Démonstration
Hypothèses :
•ABC est un triangle isocèle.
•E est le symétrique de B par rapport à A.
On note :
̂
ABC
= x.
On souhaite démontrer que
̂
EAC
= 2x.
Une première démonstration
On démontre que : BEC est rectangle en C.
Préliminaires : On a AB = AC = AE et B, A et E sont alignés.
Donc : B, C et E appartiennent au cercle de diamètre [BE].
On sait que : C appartient au cercle de diamètre [BE].
Propriété : Si le cercle circonscrit à un triangle a pour diamètre d'un triangle alors ce triangle est
rectangle.
Conclusion : BEC est rectangle en C.

On détemine les mesures de
̂
ACB
,
̂
ACE
et
̂
AEC
:
•ACB est isocèle en A donc ACB = ABC = x.
•ACB et ACE sont adjacents et complémentaires donc ACE = 90 – x
•EAC est isocèle en A donc AEC = ACE = 90 – x.
On détermine la mesure de
̂
EAC
:
Dans un triangle, la somme des mesures des angles en degré est égale à 180, donc :
̂
EAC
= 180 – (90 – x + 90 – x)
= 180 – (180 – 2x)
= 180 – 180 + 2x
= 2x
Une deuxième démonstration
On détermine la mesure de
̂
BAC
:
Dans un triangle, la somme des mesures des angles en degré est égale à 180, donc :
̂
EAC
= 180 – (x + x)
= 180 – 2x
On détermine la mesure de
̂
EAC
:
Les angles
̂
BAC
et
̂
EAC
sont adjacents et supplémentaires, donc :
̂
EAC
= 180 – (180 – 2x)
= 180 – 180 + 2x
= 2x

4. Généralisation
Hypothèses :
•Soit (C), un cercle de centre O.
•Soient A, B et C trois points de (C) tous distincts tel que
̂
BAC
soit saillant
On appelle D, le point d'intersection de [AO) et de (C) distinct de A.
On raisonne par disjonction des cas.
Trois cas peuvent se produire :
Cas 1 : D est confondu avec B ou C.

Cas 2 : D appartient à l'arc de cercle de (C) intercepté par
̂
BAC
et n'est confondu ni avec B ni avec C.
Cas 3 : D n'appartient pas à l'arc de cercle de (C) intercepté par
̂
BAC
et n'est confondu ni avec B ni
avec C.