Chapitre 07 : TRIANGLES ET QUADRILATÈRES PARTICULIERS

http://mathsreibel.free.fr 1
A
B
C
Chapitre 07 :
TRIANGLES ET QUADRILATÈRES
PARTICULIERS
I) Triangles :
1) Définitions : Triangles – Sommets – Côtés - Angles :
Un triangle est une figure qui a trois côtés.
Il est composé de trois sommets, trois côtés et trois angles.
Exemple :
Exercice :
Dans le triangle DEF ci-dessous, identifier :
- Les sommets ;
- Les côtés ;
- Les angles.
2) Méthode : Construire un triangle ABC :
Construire un triangle dont on connaît les longueurs des 3 côtés.
Exemple :
ABC est un triangle tel que AB = 2 cm, AC = 3 cm et BC = 4 cm.
1) On commence par faire
une figure à main levée.
2) On trace un coté (à la règle).
En général, on choisit le plus
long.
On nomme ses extrémités.
3) On reporte (au compas) les
longueurs des deux autres
côtés à partir de la bonne
extrémité.
4) Les deux arcs se coupent :
C’est le 3ème sommet du
triangle. On le nomme puis
on trace les côtés.
Exercice :
Tracer un triangle DEF, tel que DE = 5 cm, EF = 6 cm et DF = 5,5 cm.
Le point A est un sommet.
Le segment [AC] est un côté.
 (ou  ) est un angle.

http://mathsreibel.free.fr 2
II) Triangles particuliers :
1) Définitions : Triangle isocèle – Triangle équilatéral – Triangle rectangle :
Triangle isocèle
Triangle équilatéral
Triangle rectangle
Un triangle isocèle a deux côtés
de même longueur.
Un triangle équilatéral a trois
côtés de même longueur.
Un triangle rectangle a deux côtés
perpendiculaires.
Remarques :
1) Un triangle qui n'est ni isocèle ni équilatéral ni rectangle est dit quelconque.
2) Un triangle peut être à la fois rectangle et isocèle (cf. exemple ci-contre).
2) Propriétés : Triangle isocèle – Triangle équilatéral – Triangle rectangle :
Triangle isocèle
Triangle équilatéral
Triangle rectangle
Dans un triangle isocèle,
les angles à la base ont la même
mesure et deux côtés ont la
même longueur.
Dans un triangle équilatéral,
tous les angles ont la même
mesure et tous côtés ont la même
longueur.
Un triangle rectangle a deux côtés
perpendiculaires.
Hypoténuse
Sommet
principal
Base
Sommet
principal
Base

http://mathsreibel.free.fr 3
III) Quadrilatères :
1) Définitions : Quadrilatères – Sommets – Côtés – Angles – Diagonales :
Un quadrilatère est une figure qui a quatre côtés.
Il est composé de quatre sommets, quatre côtés, quatre angles et deux diagonales.
Exemple :
Exercice :
Dans le quadrilatère ci-contre, identifier :
- Les sommets ;
- Les côtés ;
- Les angles.
- Les diagonales.
Remarque :
On désigne un quadrilatère par ses sommets dans l’ordre où on les rencontre en suivant les côtés.
Exemples :
Quadrilatère ABCD :
Quadrilatère ABDC :
Le point A est
un sommet.
 (ou 
)
est un angle
Le segment [CB]
est un côté.
Le segment [DB]
est une diagonale.

http://mathsreibel.free.fr 4
III) Quadrilatères particuliers :
1) Définitions : Rectangle – Losange – Carré – Parallélogramme :
Rectangle
Losange
Carré
Parallélogramme
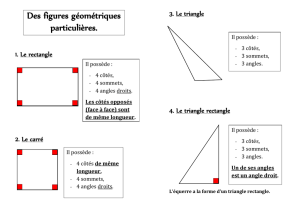
Un rectangle est un
quadrilatère qui a :
∙ 4 angles droits.
Un losange est un
quadrilatère qui a :
∙ 4 côtés de même longueur.
Un carré est un quadrilatère
qui a :
∙ 4 côtés de même longueur ;
∙ 4 angles droits.
Un parallélogramme est un
quadrilatère qui a :
∙ ses côtés opposés parallèles.
2) Propriétés : Rectangle – Losange – Carré :
Rectangle
Losange
Carré
Côtés opposés
Les côtés opposés sont :
∙ parallèles 2 à 2 ;
∙ de même longueur 2 à 2.
Les côtés opposés sont :
∙ parallèles 2 à 2.
∙ de même longueur (par définition).
Les côtés opposés sont :
∙ parallèles 2 à 2 ;
∙ de même longueur.
Diagonales
Les diagonales :
∙ se coupent en leur milieu ;
∙ ont la même longueur.
Les diagonales :
∙ se coupent en leur milieu ;
∙ sont perpendiculaires.
Les diagonales :
∙ se coupent en leur milieu ;
∙ ont la même longueur ;
∙ sont perpendiculaires.
Remarque :
Un carré est à la fois un rectangle et un losange. Il cumule donc les propriétés du rectangle et du losange.