Dipôles RC, RL, RLC : Résumé de Cours Physique

- 1 -
E
C
I- Le condensateur :
Le condensateur est un composant électrique qui peut stocker de l’énergie lorsqu’il est
chargé.
Son symbole est le suivant :
La charge d’un condensateur est par convention la charge prise par l’armature vers laquelle
est orienté le sens de courant électrique.
En courant contenu q est donnée pat la relation q = I. t.
Si le courant est variable i =dq
dt.
Pour un condensateur plan l’expression de sa capacité est donnée par la relation suivante :
C = S
e= r .o S
e .
La tension au bornes du condensateur est u C = q
C son énergie est EC = 1 2 C u C 2 = 1 2 q2 C.
uC
q
II- Le dipôle RC :
1- Réponse du dipôle RC à un échelon de tension :
Le condensateur se charge progressivement lorsqu’on applique à ces bornes un échelon de
tension E.
L’équation différentielle en q (ou en u C) est la suivante :
dq
dt + q RC = E R. ( duC dt + 1 RC uC = E RC)
La solution est de la forme : q(t) = Qo[1 – exp(- t
 )] ( uC(t) = E [1 – exp(- t  )] avec  = RC
et Qo = C.E
C
q2
Ec
K
K2
R

- 2 -
E
t
UG = E ; uC
E
R
t
i
2- Décharge d’un condensateur à travers un conducteur ohmique :
Le condensateur se décharge progressivement lorsqu’on déplace le commutateur en position
(2).
L’équation différentielle en q (ou en u C) est la suivante :
dq
dt + q RC = 0 ( duC dt + 1 RC uC = 0)
La solution est de la forme : q (t) = Qo exp(- t
 ) ( uC(t) = E exp(- t  )) avec  = RC
et Qo = C.E
E
t
uC
i (t) = -Io exp(- t
 ) avec Io= Qo
t
- E
R
i
Le condensateur est complètement chargé ou déchargé après une durée de temps
t = 4,6 ≈ 5
0
5
t
Qo
q
Qo
t
q

- 3 -
II- Le dipôle RL :
1- Réponse d’un dipôle RL à un échelon de tension :
Il s’établit progressivement un courant électrique contenu Io
dans le circuit suite à l’application d’un échelon de tension aux
bornes du dipôle RL.
Equation différentielle en i :
di
dt + 1
.i = E
L avec  = L r +R
La constante de temps  est une grandeur qui renseigne sur
le retard avec lequel le régime permanent s’établit.
E
UR = R.Io
uR(t) = UR(1-exp(-t
))
t
uR
E
ub(t) = E exp(- t
 ) + r.E
R+r(1-exp(- t
 ))
r.E
R+r
t
ub
2- Rupture d’un courant dans un circuit RL :
Equation différentielle en i :
di
dt + 1
.i = 0 avec  = L
r +R
Io = E
R+r
i(t) = Io(1-exp(-t
))
t
i
Io i(t)= Io exp (- t
)
t
i
R.Io uR(t)= R.Io exp (- t
)
t
uR

- 4 -
En régime permanent la bobine se comporte
comme un conducteur ohmique.
L’énergie magnétique restituée dans la bobine
lorsqu’elle est parcourue par un courant i est :
EL = 1
2 L.i2.
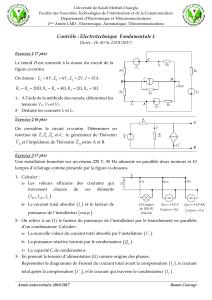
IV- Le dipôle RLC :
On charge un condensateur et on le connecte en série avec un conducteur ohmique de
résistance R2 et une bobine d’inductance L et de résistance interne r.
Equation différentielle :
Ld2q
dt2 + Ro dq
dt + q
C = 0 avec R0 = R2 + r
LC d2uC
dt2 + RoC duC dt + uC =0
Pour des grandes valeurs de Ro.
C’est le régime apériodique.
Le régime critique est un régime
apériodique qui correspond au retour
le plus rapide du système vers son état
d’équilibre.
t
uc
L’énergie totale du circuit diminue au cours du temps à cause de la résistance totale du circuit
qui dissipe l’énergie sous forme de chaleur par effet joule.
E = EL + Ec = 1
2L.i2 + 1 2 q2 C donc dE dt = i( Ldi dt + q c) = - Ro .i2 < 0
T’= T
2
Ec
EL
T’
t
E
t
ub(t)= E( r
R+r – 1) exp(- t
 )
E( r
R+r – 1)
ub
Pour des petites valeurs de R o
uC(t) c’est le régime pseudopériodique
uR(t)
T
2T
t
0
u(V)

- 5 -
Cas particulier Ro = 0.
Les oscillations dans ce cas sont libres non amorties dont l’équation différentielle est de la
forme :
Ld2q
dt2 + q C = 0 c.a.d d2q dt2 + w02 q = 0 avec w0 = 1
LC la pulsation propre des oscillations.
La période propre est To = 2 LC et la fréquence propre est No = 1
2 LC
q (t) = Qm sin(w0.t + q) avec Qm = C.Ucm
i (t) = Im sin(w0.t + i) avec Im = w0. Qm et i = q + 
2
Cas ou q = 
2 rad
To
t
i(t) et q(t)
L’énergie totale du circuit reste constante au cours du temps donc le système est conservatif.
E = EL + Ec = 1
2L.i2 + 1 2 q2 C = 1 2 LIm2 = 1 2 Qm2 C
dE
dt = i( Ld2q dt2 + q c) = 0
T =To
2
EC
EL
t
0
Ec ; EL
dE
dt = dEC dt + dEL dt = 0 donc dEC dt = - dEL dt
Les oscillations libres non amorties sont dues à une transformation mutuelle et intégralle
d’énergie électrique et énergie magnétique.