Hacheur Abaisseur: Calcul des Pertes - Exercices Corrigés
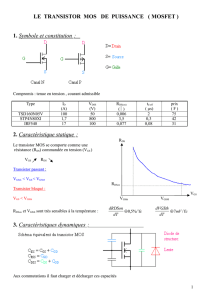
Telechargé par
El Hadji Fallou Fall Fall

Polytech’Tours DEE – 5ème année
- 1 -
Composants de puissance et applications (CPAP) – Travaux Dirigés
Séance n° 1 – « Calcul des pertes dans un hacheur abaisseur de tension »
Corrigé du problème unique
Un convertisseur DC-DC, abaisseur de tension (BUCK), fonctionne en mode continu. Les
conditions d’application sont les suivantes :
Tension d’entrée : VIN = 100 V.
Tension d’alimentation du MOSFET : VDD = 15 V.
Fréquence de fonctionnement : F = 200 kHz.
Rapport cyclique : α = 0,5.
Courant dans l’inductance au moment de la fermeture du transistor : IFM = 8 A.
Vitesse de fermeture du transistor : dI/dt = 100 A/µs.
Température ambiante maximale : 75°C.
Les inductances parasites sont négligeables.
On utilise une diode rapide BYW29 et un MOSFET IRF640 (cf. Documentations techniques).
On supposera les courants de forme rectangulaire et d’amplitude IFM. À la fermeture, on admettra
que la tension aux bornes du MOSFET décroît instantanément dès que la diode de roue libre se
bloque (ID = IRM).
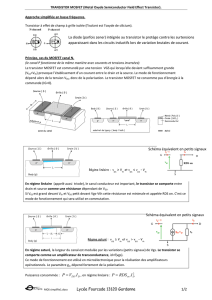
1) Tracer le schéma et les formes d’ondes simplifiées
du fonctionnement du hacheur.
Schéma de principe du hacheur série +
chronogrammes de fonctionnement :

Polytech’Tours DEE – 5ème année
- 2 -
2) Calculer les pertes statiques dans la diode.
Rappel des pertes dans la diode. On distingue les pertes statiques (ON et OFF) et les
pertes en commutation :
Pertes en conduction :
- α = 0,5 et IFM = 8 A ⇒ IF(AV) = (1 – α) × IFM = 4 A.
- IF(RMS) = racine.carrée((1 – α) × (IFM))²) ≈ 5,7 A.
- Pcond ≈ 3,9 W.
Pertes en inverse << Pertes en conduction
3) Calculer les pertes dues à la commutation dans la diode.
Pertes à l’ouverture :
- dI/dt = 100 A/µs ⇒ IRM ≈ 4,5 A.
I
RM
≈ 4,5 A

Polytech’Tours DEE – 5ème année
- 3 -
- WOFF = 0,5 × tb × VIN × IRM.
- tb = 50 ns ⇒ WOFF ≈ 11,3 µJ ⇒ POFF = WOFF × F ≈ 2,3 W.
Pertes à la fermeture :
- VFP = 2 V, VFM = 0,9 V, IFmax = 8 A, tfr = 15 ns et F = 200 kHz ⇒ PON ≈ 10,6 mW.
V
FM
≈ 0,9 V

Polytech’Tours DEE – 5ème année
- 4 -
Conclusion : Pertes totales ≈ 6,2 W.
4) En déduire la résistance thermique maximale que l’on doit ajouter (ou non) au boîtier de la
diode.
Rth(j-a) MAX = (Tjmax – Tamax) / Pertes ≈ (150 – 75) / 6,2 ≈ 12,1°C/W ⇒ REFROIDISSEMENT
CUIVRE IMPOSSIBLE.
Dimensionnement du dissipateur thermique avec une diode en boîtier TO-220 : Rth(j-a) MAX =
Rth(j-c) + Rth(c-h) + Rth(h-a). On néglige la résistance thermique Rth(c-h) (graisse thermique). Rth(h-a)
MAX = Rth(j-a) MAX – Rth(j-c) ≈ 12,1 – 2,8 = 9,3°C/W.
Dans la pratique, on prend un dissipateur dont la résistance thermique est inférieure ou
égale à 9,3°C/W.
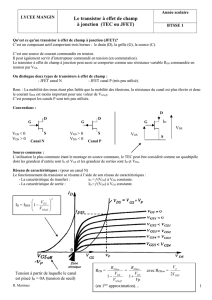
5) Déterminer la résistance de grille (valeur normalisée) pour avoir une vitesse de fermeture
du transistor de 100 A/µs ?
dI/dt = 100 A/µs ⇒ IRM ≈ 4,5 A.
Donc : IFM + IRM ≈ 8 + 4,5 ≈ 12,5 A.
Donc : ΔVGS = ΔID / GFS ≈ 12,5 / 11 ≈ 1,1 V.
VGS(th) ?

Polytech’Tours DEE – 5ème année
- 5 -
VGS(th) = 3 V (en valeur typique).
VGS(plateau) = VGS(th) + ΔVGS ≈ 3 + 2,2 ≈ 5,2 V.
VGS(t) = VDD × (1 – exp[-t / (RG × Ciss)] )
Pour t = tinitial ⇒ VGS(t) = VGS(th) ≈ 3 V ⇒ tinitial = - RG × Ciss × ln(1 – (VGS(th) / VDD)).
Pour t = tfinal ⇒ VGS(t) = VGS(plateau) ≈ 5,2 V ⇒ tfinal = - RG × Ciss × ln(1 – (VGS(plateau) / VDD)).
Conclusion : Δt = tfinal – tinitial = - RG × Ciss × ln((1 – VGS(plateau)) / (1 – VGS(th))).
GFS × ΔVGS / Δt < 100 A/µs ⇒ RG > (GFS × ΔVGS) / (-Ciss × dI/dt × ln((1 – VGS(plateau)) / (1 – VGS(th))))
⇒ RG > 996 Ω (avec Ciss = 1200 pF) ⇒ RG > 1 kΩ.
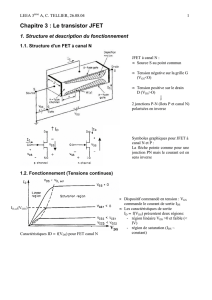
6) En déduire les valeurs des fronts de tension (ON et OFF) ainsi que le dI/dt au blocage.
Q2 Q4 Q
(pour Ig=cte)
VGS(Mil)
G
S
D
Cgd
Cgs
VGS
Ig
Vdd
Io
ID
VDS
VGS(th)
VGS
t
t1t0 t2 t3
VDS ID
Vdd
VDS(on)
Io
t4
Q3
Q1 Q2 Q4 Q
(pour Ig=cte)
VGS(Mil)
G
S
D
Cgd
Cgs
VGS
Ig
Vdd
IoIo
ID
VDS
VGS(th)
VGS
t
t1t0 t2 t3
VDS ID
Vdd
VDS(on)
Io
t4
Q3
Q1
≈ 0,73
 6
6
 7
7
1
/
7
100%