3D Image Reversible DWT via Pyramid Method

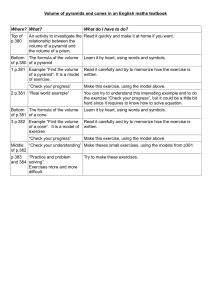
Abstract— In this research, the pyramidal structure and algorithm are
proposed for computing the reversible discrete wavelet transformation
of 3D Image. The concept of formal language is used to emphasis the
modeling of a pyramidal structure of forward and reverse transform.
With the assumption, the pyramid representation can help the 3D
Image representation and can facilitate the processing.
Keywords— Discret Wavelet Transform, Pyramid Method,
Pyramidal Data Structure and Algorithm, Tree-Dimension.
I. INTRODUCTION
MAGE processing based on Discrete Wavelet Transformation
(DWT) and using pyramidal techniques, as reveal Adelson et
al [1], is nowadays essential. Discrete Wavelet
Transformation (DWT), as stated in [2], proceed a signal has a
cut-of-frequency and it is computed by successive Lowpass and
Highpass filtering of the discrete time-domain signal. Filters are
signal processing functions. Furthermore, a measure of the
amount of detail information signal is determined by the
filtering operation (Lowpass and Highpass) and the scale is
detrmined by Upsampling and Downsampling.
The pyramidal technique is a type of multi-scale signal
processing in which a signal or an image is subject to repeated
smoothing and subsampling [3].
Practically, for representing a three dimensional image (3D
Image) , we can refer to a three dimensional Euclidian space as
stated in [4].
In this research, the pyramidal structure and algorithm are
proposed for computing the reversible discrete wavelet
transformation of 3D Image. The concept of formal language is
used to emphasis the modeling of a pyramidal structure of
forward and reverse transform. With the assumption, the
pyramid representation can help the 3D Image representation
and can facilitate the processing.
II. PYRAMID METHOD OF 3D DWT
A. Overview
For our purpose, the 3D DWT is based on the method of
inferring 3D image information into a smaller non-overlapping
tiles on which 2D DWT can be applied.
The reversible DWT as show in figure 1, has two main
phases: Decomposition and reconstruction phases.
In decomposition phase, the DWT can be done by iteration
of filtering and Downsampling operation. In reconstruction
phase, the DWT is the reverse process of decomposition in that
the original signal is then obtained by iteration of Upsampling
and filtering operation
A 3D image is a set of sequence of sample values
I=[ xi, yj, zk], where 0 ≤ xi ≤ N1, 0 ≤ yj ≤ N2, 0 ≤ zk ≤ N3; xi, yj
and zk are the integers that having finite extents, N1, N2 and N3,
in the horizontal, vertical and depth directions, respectively. A
2D image is a set of sequence of sample values I’=[ xi, yj],
where 0 ≤ xi ≤ N1, 0 ≤ y j≤ N2. A digitized 3D image size is in
N1 X N2 X N3 and a sub block is in size 1/2n X 1/2n X 1/2n.
With respect to a fixed global reference frame, it is possible to
make correspondence between points in 3D space and their
projected images in a 2D image plane, with respect to a local
coordinate frame.
Fig. 1 Reversible DWT of 3D
B. Formalization
For representing the DWT of 3D Image, we refer to formal
language and regular images [5]. We assume that the computer
has finite memory, so there are only finitely many states the
computer can be at, and the previous state of the computer
determines the next state, so the machine has deterministic state
transitions.
The concept of language theory serves as basis to emphasis
the problem related to reversible 3D DWT. We consider the
following definitions:
The formal language L is composed by an alphabet ∑ and a
specific grammar G.
Definition 1: Language
Let an alphabet ∑ be a set of element, ∑ ={H, L}, that
represents the high and low frequencies.
Definition 2: Alphabet
The grammar is given by a 5-tuple:
Definition 3: Grammar
G={VN, VT, I, F,C}
with VN={I, W}, VT={Hx, Hy, Hz, Lx, Ly, Lz}, where G denotes
a grammar; VN denotes a Non Terminal Verb; VT denotes a
Pyramid Method for Reversible Discrete
Wavelet Transformation of 3D Image
Eustache Muteba Ayumba
I
3D
Original
Image
Forward
DWT
2D
DWT
Reverse
DWT
3D
Restore
Image
Latest Trends on Systems - Volume I
ISBN: 978-1-61804-243-9
382

Terminal nodes expressing low and high frequencies in all
direction, X, Y and Z; I denotes an input image; F denotes the
formula with a set of constraints C attached to each terminal
node to code the word. In order to achieve perfect
reconstruction the analysis and synthesis filters have to satisfy
certain conditions.
The formula generates word from a terminal verb:
Definition 4: Formula
F={I → W}; W=w Wm , m>=1
Thus, there is a specification language L for representing 3D
DWT as a text that is a set of sentences S. The respective text
should be described as follows:
Text := S{S}*
S := W{W}*
W := w{w}*
w := ‘Hx’ |‘Hy’| ‘Hz’ | ‘Lx’ | ‘Ly’ | ‘Lz’
It is possible by means of sentences to keep track of image
information.
III. PYRAMIDAL DATA STRUCTURES AND
ALGORITHMS
A. Data Structures
The data structure used to represent image information can be
critical to the successful completion of an image processing
task. The structure of reversible 3D DWT as showed in figure
2 express all operations of filtering and scaling along the three
direction saying width direction, height direction and depth
direction at decomposition and reconstruction phases. This
pyramidal structure representation is suitable to a tree structure.
Therefore, it is, also, possible to use pointers, as data type, at
each node in order to improve performance in repetitive
operations.
Given an input 3D image, with respect to our language L, we
can organize it in hierarchical tree structure where each
terminal node corresponds to a sub block as shown bellow.
Thus, any word in the language can be parsed by the grammar
that has three levels of related image information to the start
node, the original image.
Fig. 2 Structure of the reversible 3D DWT
B. Algorithms
Our algorithm is based on the purpose of overview in section
2 and is a consequence of the pyramidal data structure
presented in section 3.
For a given image I=[ xi, yj, zk], where 0 ≤ xi ≤ N1, 0 ≤ yj ≤
N2, 0 ≤ z k ≤ N3; Let dwt (discrete wavelet transform) be a
recursive function that computes I on l level, l>=1:
)(
1Idwtdwt m
l
∑
=
=
(1)
Firstly, we use the function dwt and process a low-pass
decomposition and high-pass decomposition in the width
direction (horizontal details), after in the height direction
(vertical details) and at last in depth direction.
Filtering and scaling along Direction X: Lx, Hx
)))),,
2
())(,,
2
((((
12 1
3
32
1
32
1
1 11
1∑∑ ∑∑ = ==
=N
x
N
y
N
xx
N
zNN
N
HNN
N
Ldwt
(2)
Filtering and scaling along Direction Y: LxLy, LxHy, HxLy,
HxHy
∑ ∑ ∑ ∑∑∑
= = = ===
=
1 2 1 22
1 2 1
2
1
3
21
3
21
12
3
21
3
21
2
)))),
2
,
2
()))(,
2
,
2
((())()),
2
,
2
()))(,
2
,
2
(((
N
x
N
y
N
x
N
yyxyx
N
y
N
yyxyx
N
NN
LHN
NN
HHN
NN
HLN
NN
LLdwt
(3)
Filtering and scaling along Direction Z: LxLyLz, LxLyHz,
LxHyLz, LxHyHz, HxLyLz, HxLyHz, HxHyLz, HxHyHz (4)
))))
2
,
2
,
2
())(
2
,
2
,
2
((((()))
2
,
2
,
2
())(
2
,
2
,
2
(((((
))))
2
,
2
,
2
())(
2
,
2
,
2
((((()))
2
,
2
,
2
()()
2
,
2
,
2
(((((
1 2 3
1 2 3
1 2 3 1 2 3
1 1
3
21
3
21
11 1
3
21
3
21
1
1 1
3
21
3
21
11 1
3
21
1
3
21
3
∑ ∑ ∑∑ ∑ ∑
∑ ∑ ∑∑ ∑ ∑
= = == = =
= = == = =
=
N
x
N
yzyx
N
zzyx
N
x
N
yzyx
N
zzyx
N
x
N
yzyx
N
zzyx
N
x
N
yzyx
N
zzyx
N
NN
HHH
N
NN
LHH
N
NN
HLH
N
NN
LLH
N
NN
HHL
N
NN
LHL
N
NN
HLL
N
NN
LLLdwt
Secondly, we use the reverse function dwt' and process a low-
pass reconstruction and high-pass reconstruction in the width
Lx
Hx
LxLy
HxHy
LxHy
HxLy
LxLyLz
LxLyHz
LxHyLz
LxHyHz
HxLyLz
HxHyHz
HxHyLz
HxLyHz
Original
Image
Downsample or
Upsample along
Direction X
Downsample or
Upsample along
Direction Y
Downsample or
Upsample along
Direction Z
Lowpass
Filtering /
Scaling
Highpass
Filtering /
Scaling
Latest Trends on Systems - Volume I
ISBN: 978-1-61804-243-9
383

direction (horizontal details), after in the height direction
(vertical details), and at last in depth direction.
The algorithm is highly memory efficient due to fact that the
3D size is limited. Also, the computation complexity has
acceptable processing time.
IV. CONCLUSION
The image coding methods using wavelet transform and
pyramidal technique is essential and really efficient in image
processing [6], [7].
One of the important contributions of our paper is the
pyramidal data structure and algorithm for 3D (DWT) image
processing. This is method can be used efficient in the filed of
medical science and Biotechnology.
REFERENCES
[1] E.H. Adelson, C.H. Anderson, J.R. Bergen, P.J. Burt & J.M. Ogden,
“Pyramid methods in image processing”, 1984. Available:
http://persci.mit.edu/pub_pdfs/RCA84.pdf
[2] T. Edwards, “Discrete Wavelets Transforms: Theory and
Implementation”, 1992. Available:
http://qss.stanford.edu/~godfrey/wavelets/wave_paper.pdf
[3] Wikipedia, ”Pyramid (image processing)”. Available:
http://en.wikipedia.org/wiki/Pyramid_(image_processing)
[4] Y.H. Lee, S.J. Horng, J. Seitzer, “Parallel Computation of the Euclidean
Distance Transform on Tree-Dimensional Image array” in IEEE
Transactions on Parallel and Distributed Systems, vol. 14, NO. 3, March
2003, pp 203-212.
[5] S. Wintner, “Formal Language Theory for Natural Language Processing”,
2001. Available:
http://www.helsinki.fi/esslli/courses/readers/K10.pdf
[6] E. H. Adelson, C. H. Anderson, J. R. Bergen, P. J. Burt, J. M.
Ogden, “Pyramid methods in image processing”. Available:
https://alliance.seas.upenn.edu/~cis581/wiki/Lectures/Pyramid.pdf
[7] B. K. Choudhary, N. K. Sinha, P. Shankera, “Pyramid Method in
Image Processing”, in Journal of Information Systems and
Communication, Volume 3, Issue 1, 2012, pp.- 269-273.
Available: http://www.bioinfo.in/contents.php?id=45
Latest Trends on Systems - Volume I
ISBN: 978-1-61804-243-9
384