Flot

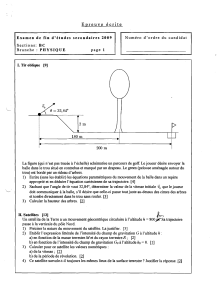
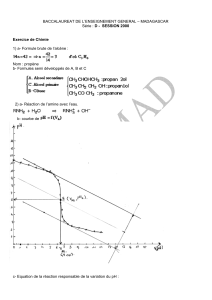
Chapitre II
Rappels sur les equations differentielles
Nous indiquons dans ce chapitre les notions sur les equations differentielles dont
nous aurons besoin dans la suite. Pour la plupart, ces notions sont enseignees en
licence de mathematiques; elles sont rappelees ici sans demonstration. Le lecteur
pourra trouver ces demonstrations dans tout cours de calcul differentiel, comme par
exemple [18].
Certains resultats, malheureusement pas toujours enseignes en licence malgre leur
importance, sont presentes avec leur demonstration. Il en est ainsi par exemple du
theoreme des bouts (3.3), de la proposition relative a l'image directe
d'un champ de
vecteurs (5.1) et du theoreme de redressement local (5.2).
Pour les equations differentielles satisfaisant les hypotheses du theoreme de Cauchy-
Lipschitz, nous introduirons (paragraphe 4) les concepts de
flot et (pour les equations
autonomes) de flot reduit. Nous verrons que les applications partielles construites
avec le flot (ou le flot reduit) constituent un systeme dynamique a temps continu,
naturellement associe a l' equation differentielle. Dans le cas ou
l' equation est
autonome, le champ de vecteurs qui lui est associe n'est autre que le generateur
infinitesimal de ce systeme dynamique.
1. Equations differentielles sous forme canonique
1.1. Notations et conventions. -Dans ce paragraphe t: est un espace affine reel, dont
l'espace vectoriel associe E est muni d'une norme. Nous devrons supposer parfois (par
exemple dans l'enonce du theoreme de Cauchy-Lipschitz 2.8), de plus, que l'espace
norme E est complet, c'est-a-dire est un espace de Banach. Rappelons que cette
condition est automatiquement satisfaite lorsque E est de dimension finie. Rappelons
aussi que toute application lineaire de
JR. dans E est automatiquement continue et
que l'espace
.C(!R., E) de toutes les applications lineaires de JR. dans E est un espace
vectoriel norme qui s'identifie a
E, grace a l'isomorphisme conservant la norme qui,
a un element
<p de .C(IR., E), associe l'element <p(l) de E. L'isomorphisme reciproque
associe, a chaque element x de
E, l'application lineaire t f------t tx de JR. dans E. Nous
utiliserons systematiquement cette identification. De meme, nous identifierons les espaces
.C(!R., .C(IR., E)), .C ( JR., .C (JR., .C(!R., E))), etc ... , a E. Une application <p d'un intervalle
ouvert I de
JR. dans t: etant donnee, nous noterons <p
1,
<p
11
, •• • , <p(n) ses derivees premiere,
seconde,
... , d' ordre n, lorsqu' elles existent. Nous noterons aussi, occasionnellement, !~,
d2 1/l dntll
r r d' · ' 1 · A 1 d R 1
dt2 , ... , dtn ces envees, orsque ces notations paraitront p us commo es. appe ons
que lorsque
l' application <p est n fois differentiable sur I, ses derivees <p
1,
<p
11
, ••• ,
<p(n) sont des applications de I, respectivement, dans .C(JR., E), .C(!R., .C(!R., E) ), ... ,
.c( JR., .C(!R., .C( ... E) .. . ) ) . Mais compte tenu des identifications mentionnees ci-dessus,
nous pouvons considerer toutes les derivees
<p
1,
<p
11
, ••• , <p(n) de l'application r.p comme
etant a valeurs dans E.

§ 2. Le theoreme d'existence et d'unicite 19
1.2. Definitions. - Une equation differentielle du premierordre, sousforme canonique,
dans l'espace affine t: d'espace vectoriel associe E, est une relation de la forme
cp'(t) = J(t, cp(t)), (1)
oiz fest une application d'une partie fi de JR x t: dans E. Une solution (ou courbe
integrate) de cette equation differentielle est une application differentiable
cp d'un
intervalle ouvert I de
JR dans £ telle que, pour tout t EI, (t, cp(t)) soit element de
fi et que (t, cp(t), cp'(t)) verifie la relation (1).
1.3. Definitions. -Une equation differentielle autonome du premier ordre, sousforme
canonique, dans l'espace
affine£ d'espace vectoriel associe E, est une relation de
la forme
cp'(t) = X(cp(t)), (2)
oiz X est un champ de vecteurs sur une partie Ode£, c'est-a-dire une application
de O dans
E. Une solution (ou courbe integrate) de cette equation differentielle est
une application differentiable
cp d 'un intervalle ouvert I de JR dans £ telle que,
pour
tout t EI, cp(t) soit element de O et que (cp(t), cp'(t)) verifie la relation (2).
Les solutions (ou courbes integrales) de l'equation differentielle autonome (2) sont
aussi appelees courbes integrates du champ
de vecteurs X.
En d' autres tennes, une equation differentielle du premier ordre, sous fonne canonique,
de la fonne ( 1), est autonome si la partie fi de
JR x t: sur laquelle l' application f est definie
est de la fonne
JR x 0, ou O est une partie de t:, et si, pour chaque x E 0, la fonction fest
constante sur la partie JR x { x} de JR x 0. On dit alors que f ne depend pas de sa premiere
variable t E R
La proposition suivante indique une importante propriete de !'ensemble des solutions
d'une equation autonome.
1.4. Proposition. -Soit
cp : I -----+ E une solution de l'equation differentielle
autonome (2) et soit t0 ER Designons par Tt0 : JR-----+ JR la translation
t f---4 Tt0(t) = t -to.
Alors l'application
cp o Tt 0 du translate I+ to de l'intervalle I dans E est aussi
solution de l'equation autonome (2).
Preuve: Voir par exemple [18], chapitre IV, paragraphe 2.2. D
2. Le theoreme d'existence et d'unicite
Soit t: un espace affine reel dont l'espace vectoriel associe E est muni d'une nonne, et f
une application d'une partie n de JR X t: dans E. On considere !'equation differentielle
cp'(t) = f(t,cp(t)). (1)
2.1. Definition. - Une solution cp : I -----+ t: de l'equation differentielle (1) est dite
maximale si toute solution de (1) dont l'intervalle de definition contient I et dont
la restriction a I coincide avec cp est egale a cp.
2.2. Definitions. -Une donnee de Cauchy pour ]'equation differentielle (1) est un
point
(to, Xo) de la partie n de JR X t: sur laquelle est definie cette equation. On
dit qu'une solution
cp: I-----+ t: de l'equation (1) satfafait la donnee de Cauchy (to, xo)
si
to EI et cp(to) = xo.
On appelle probleme
de Cauchy la recherche d'une solution de l'equation (1)
satisfaisant une donnee de Cauchy specifiee ( t0, x0 ).

20
Chapitre II. Rappels sur les equations differentielles
2.3. Definition. -Soit (to, Xo) E n. On appelle tonneau de securite ouvert (resp.,
ferme) de centre (to, x0) une partie
de~ x t: de la forme Io x B0, ou 10 est un
intervalle ouvert (resp., ferme) de centre t0, de longueur 2l > 0, et Bo une boule
ouverte (resp., fermee) de centre x0, de rayon r >
0, telle que
Io x Bo c n et sup IIJ(t,x)/1 < y.
(t,x)EloXBo
2.4. Remarques
a) Gas ou f est locaJ.,ement bornee. -Si f ~st localement bomee sur n, et en particulier
si
fest continue sur n, tout point interieur an est centre d'un tonneau de securite. Soit en
effet (to,
Xo) Un point interieur 3. 0. Puisque j est localement bomee, iJ existe Un YOisinage
W de (to,xo) dans n sur lequel fest bomee; ii existe done unreel M > 0 tel que
SUP(t,x)EW II! (t, X) II < M. Puisque (to, Xo) est interieur an, le voisinage w de (to, xo)
dans nest aussi voisinage de (to, xo) dans x t:. L'ensemble des parties de~ x t: de la
forme
[to-l, t0 +l] x Bp(x
0,
lM), avecl > 0, estun systeme fondamental de voisinages
de (to, x0) dans x
t: (nous avons note Bp(x
0,
lM) la boule fermee de£, de centre x0 et
de rayon
lM). Pourl > 0 assez petit, nous avons done [to -l, t0 +l] x Bp(x
0,
lM) c W,
et nous voyons que [to -l, t0 + l] x Bp(x
0,
lM) est un tonneau de securite ferme centre
sur le point (to, xo). Bien entendu,
]to -l, to+ l[xB(xo, lM), ou B(xo, lM) designe
la boule ouverte de
t: de centre x0 et de rayon lM, est un tonneau de securite ouvert de
centre (to,xo).
b) Homotbetique d'un tonneau de securite. -Soit Io x Bo un tonneau de securite
(par exemple ferme) de centre (to, x0
). Notons Io = [to -l, t0 + l], B0 = Bp(x
0,
r),
avec l > 0, r > 0. Tout point (t1,x1) de O interieur a Io x Bo, c'est-a-dire verifiant
lti - tol < let llx1 - xoll < r, est aussi centre d'un tonneau de securite Ii x B1. II suffit
de prendre
Ii = [t1 - li, t1 + li], B1 = Bp(x1, r1), en choisissant Li et r1 de maniere
telle qu'ils verifient
r1 r
li l' O<li:S:l-lt1-tol, O<r1:S:r-llx1-xoll-
Ces conditions impliquent en effet Ii x B1 c Io x B0 c n, done
sup IIJ(t,x)II :s; sup IIJ(t,x)II < ~l = rl1.
(t,x)Eli xB1 (t,x)EloxBo 1
Cette remarque est souvent utile pour l'etude de !'existence des solutions d'une equation
differentielle.
c) Interet des tonneaux de securite. -Soit <p : I - t: une solution de I' equation
differentielle (1) satisfaisant la donnee de Cauchy (to, x0
). L'existence d'un tonneau de
securite
Io x Bo de centre (to, xo) E x t: permet de montrer que le graphe de la
restriction de
<pa In Io est contenu dans ce tonneau de securite. C'est ce qui resulte du
lemme suivant, et
c'est la le principal interet de la notion de tonneau de securite.
2.5. Lemme. -Soit <p : I - t: une solution de l'equation differentielle (1)
satisiaisant la donnee de Cauchy (t0 ,x
0
). S'il existe un tonneau de securite (par
exemple ouvert)
Io x Bo de centre (to, xo), la solution <p verifi.e, pour tout t E InI
0,
llcp(t) - <p(to) II < r,
ou r > 0 est le rayon de la boule Bo. Cela exprime que le graphe de la restriction
de <pa
In Io est contenu dans Io x B0.

§ 2. Le theoreme d'existence et d'unicite
21
Preuve : Soit 21 > 0 la longueur de l'intervalle 10• D'apres la definition d'un tonneau
de securite, nous avons
sup IIJ(t,x)II = M < y.
(t,x)EloxBo
Supposons qu'il existe ti E In Io tel que llcp(t1) - cp(to) II :::=: r. Necessairement, t1 -=I to;
supposons par exemple ti > t0• Posons
tM = sup{ t E Info; t :::=:to, VOE [to,t], llcp(O)- cp(to)II < r}.
Le reel tM existe, car c'est la borne superieure d'une partie de JR non vide (elle contient to)
et majoree par ti. 11 appartient a l'intervalle [to, ti], done a In Io. Puisque cp est continue,
nous avons
llcp(tM)- cp(to)II = r. (*)
D'autre part, d'apres la definition meme de tM, pour tout t E [to,tM[, (t,cp(t)) est
element de
Io X Bo, done
llcp'(t)II = IIJ(t, cp(t))II :s: M < y.
Mais alors, d'apres le theoreme des accroissements finis,
llcp(tM) - cp(to)II :S: M!tM - to! :S: Ml< r,
ce qui contredit ( * ).
D
2.6. Definitions. -Soient E et F deux espaces vectoriels normes, ou deux espaces
afH.nes dont les espaces vectoriels asssocies sont normes.
1. Une application f, definie sur une partie O de E et a valeurs dans F, est dite
lipschitzienne s'il existe un reel k
:::=: 0 tel que, pour tous xi et x2 E 0,
IIJ(x2) - f(xi) II :S: kllx2 - xi II.
Le reel k est appele rapport de l'application f. On dit alors aussi que f est k-
lipschitzienne pour dire qu'elle est lipschitzienne de rapport k.
2. Dans les memes hypotheses, on dit que l'application f est localement lipschitzi-
enne si tout point x de O possede un voisinage ( dans O) tel que la restriction de f
ace voisinage soit lipschitzienne, son rapport pouvant dependre du point x.
3. Soit A un ensemble, et g une application definie sur une partie O de Ax E,
a valeurs dans F. On dit que f est lipschitzienne relativement a sa seconde variable
x E E s'il existe un reel k
:::=: 0 tel que, pour tout a E A, tous x1 et x2 E E tels que
(a,xi) et (a,x2) soient elements den,
llg(a,x2) -g(a,x1)II :S: kllx2 -xiii.
4. On suppose de plus l'ensemble A muni d'une topologie. L'application g est
dite
local,ement lipschitzienne relativement a sa seconde variable x E E si tout point
(
a, x) E O possede un voisinage W c A x E tel que la restriction de f a On W soit
lipscbitzienne relativement a
sa seconde variable (son rapport pouvant dependre
du point (a,x) E O considere).
2.7. Exemple important. -Soit £ un espace affine dont l'espace vectoriel associe
E est norme et f une application definie sur un ouvert n de
JR X £' a valeurs dans un
autre espace vectoriel norme F. Si f est differentiable de classe
GP, avec p :::=: 1, elle
est localement lipchitzienne par rapport a sa seconde variable ( et meme par rapport a
l 'ensemble ( t, X) E n des deux variables dont elle depend). Cela resulte en effet aisement
de l'inegalite des accroissements finis.

22 Chapitre II. Rappels sur les equations differentielles
2.8. Theoreme de Cauchy-Lipschitz. -Soit £ un espace affine dont l'espace
vectoriel associe E est un espace de Banach reel, et f : n
-----+ E une application
d'une partie n de
lll X £ dans E. On considere l'equation dilferentielle
cp'(t) = f(t, cp(t)). (1)
Soit (to, xo) E r2 une donnee de Cauchy, qu'on suppose centre d'un tonneau
de securite ferme
Io x Bo contenu dans r2 (avec Io = [to -l, to + l], l > 0,
Bo = BF(x
0, r), boule fermee de centre
xo et de rayon r > 0). On suppose aussi
la restriction de f a
Io x Bo continue, et lipschitzienne relativement a sa seconde
variable.
11 existe alors une solution de l'equation differentielle (1) satisfaisant la
donnee de Cauchy (to, x0
), defi.nie sur l'intervalle ouvert ]t
0
-l, t0 +l[. Cette solution
est unique, au sens suivant : toute autre solution de l'equation differentielle
(1)
satisfaisant la meme donnee de Cauchy (to, x0) coincide avec elle sur l'intersection
de son intervalle de definition avec l'intervalle
]to -l, t0 + l[.
Preuve : Voir par exemple [ 18], chapitre V, paragraphe 2. 7. D
2.9. Theoreme d'existence et d'unicite globales. -Soit £ un espac!!_ affine
dont l'espace vectoriel associe E est un espace de Banach reel,
et f : n -----+ E
une application d'un ouvert n de lll x £ dans E. On suppose f continue sur
n et localement lipschitzienne par rapport a sa seconde variable. On considere
l'equation differentielle
cp'(t) = f(t,cp(t)). (1)
Pour toute donnee de Cauchy (to, Xo) En il existe une solution maximale unique
de l'equation differentielle
(1) satisfaisant cette donnee de Cauchy.
Preuve : Voir par exemple [ 18], chapitre V, paragraphe 2.10. D
3. Bouts d'une solution maximale
Nous considerons dans ce paragraphe !'equation differentielle, dans l'espace affine£ dont
l'espace vectonel associe E est norme,
cp'(t) = J(t,cp(t)), (1)
ou fest une application d'une partie n de lll x £ dans E. Les hypotheses sur E et f seront
precisees en temps utile.
3.1. Definition. -Soit cp une solution maximale de l'equation differentielle (1),
]a, b[ son intervalle de definition (a pouvant etre fi.ni OU egal a -oo, et b fi.ni OU
egal a +oo ). On appelle bout droit (resp., bout gauche) de cette solution maximale
l'ensemble des valeurs d'adherence, lorsque t
-----+ b (resp., lorsque t -----+ a), de
l'application de
]a, b[ dans lll x £ : t 1-----+ (t, cp(t)).
3.2. Commentaires
a) Projection des bouts sur le Eacteur R - Il importe de remarquer que le bout droit
(resp., gauche) de la solution
cp est une partie de lll x £, qui peut eventuellement etre vide.
Si cette partie est non vide, sa projection sur le facteur
lll est necessairement le singleton
{ b} (resp., le singleton
{a}); en effet, b (resp., a) est la limite, done l'unique valeur
d'adherence, de !'injection canonique de
]a, b[ dans lll, t 1-----+ t, lorsque t -----+ b (resp.,
lorsque
t-----+ a).
Nous voyons done que si b = +oo (resp., si a= -oo), le bout droit (resp., gauche) de la
solution
cp est vide.