LO6 Anneaux de Newton

1
LO6 Anneaux de Newton
I. Principe
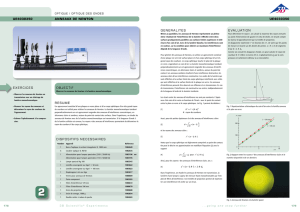
Dans un appareil à anneaux de Newton, la lumière monochromatique interfère dans le film d'air mince
entre la lentille légèrement convexe et une plaque de verre à face parallèle. Les longueurs d'onde sont
déterminées à partir des rayons des anneaux d'interférence.
II. Équipement
1 Appareil : anneaux de Newton 08550-00
1 Objectif, monté, f = +50 mm 08020-01
1 Filtre interférentiel, jeu de 3 08461-00
1 Ecran, translucide, 250 x 250 mm 08064-00
1 Lampe, f. 50 W Hg lampe haute pression 08144-00
1 Alimentation pour lampe Hg CS / 50 W 13661-97
1 Condenseur double, f = 60 mm 08137-00
2 Porte-lentille 08012-00
4 Glissière f. opt. banc d'essai, h = 30 mm 08286-01
1 Glissière f. opt. banc d'essai, h = 80 mm 08286-02
1 banc de profil optique, l = 1000 mm 08282-00
2 Base f. opter. profil-banc, 08284-00
1 Règle, plastique, l = 200 mm 09937-01
III. Tâches et objectifs
En utilisant l'appareil à anneaux de Newton, mesurer le diamètre des anneaux à différents longueurs
d'onde et:
1. déterminer les longueurs d'onde pour un rayon de courbure donné de la lentille
2. déterminer le rayon de courbure à des longueurs d'onde données.

2
IV. Théorie et évaluation
Si deux trains d'ondes à phase verrouillé de même fréquence et du même plan de polarisation (lumière
cohérente) se chevauchent, une interférence se produit après avoir parcouru des trajets différents. Pour
un angle d’ouverture limitée γ, une condition de cohérence est bien vérifiée pour une surface de
diamètre a :
a⋅sin γ≪ λ/2 (λ est la longueur d'onde de la lumière)
Des interférences dont la luminosité varie suivant les endroits peuvent survenir.
"Les anneaux de Newton" se produisent à travers la lumière monochromatique interférant dans film
mince intermédiaire entre une lentille plan-convexe et une plaque de verre à face parallèle. Le rayon 1
réfléchi sur le dessous de la lentille interfère ainsi avec le rayon 2 réfléchi au sommet de la plaque de
verre (figure ci-dessous).
Le film d'air, à une distance r du point de contact, entre la lentille et la plaque de verre a une épaisseur
D=d±d0. Comme le contact n’est pas idéal, il faut prendre d0 en considération. d0 est positif si, par
exemple, il y a des particules de poussière entre la lentille et la plaque de verre, mais peut aussi être
négatif lorsque la pression est plus grande. La différence de marche géométrique δ' des rayons
interférents (1 et 2) est donc:
δ′=2(d ±d0)
De plus, le rayon réfléchi par la surface du verre plane subit un déphasage π parce qu’il a fait la
transition d’un milieu optiquement plus mince a un milieu optiquement plus dense. L'effet de cette
correspond à une distance parcourue de longueur λ/2. En tout, il y a donc une différence de marche
égale à :

3
δ=2(d±d0)+λ/2 (1)
Pour les anneaux d'interférence nulle,
δ=2(d±d0)+λ/2=(n+1/2)λ ou 2(d±d0)=λn (2)
Conformément à la figure 3, il existe une relation entre le rayon rn du nième anneau noir, l'épaisseur d et
le rayon de courbure R de la lentille plan-convexe (dans le cas idéal d0 = 0).
d⋅(2R-d)=rn 2 (3)
Dans le cas de lentilles légèrement convexes, d<<R, nous avons pour les anneaux noir et sombre, en
utilisant (2) et (3) :
rn2 =nRλ±2 d0R (4)

4
V. Installation et procédure
L'expérience des anneaux de Newton est montée comme le montre la figure ci-dessous.
1. La lampe de haute pression à vapeur de mercure avec le double condenseur (distance focale 60
mm), le porte-lentille, le filtre d'interférence, l'appareil d’anneaux de Newton, le porte-lentille
avec la lentille de distance focale 50 mm et un écran transparent placé à environ 40 cm de
l'objectif sont tous mis en place sur le banc optique.
2. Ajuster d’abord le faisceau sans filtres de couleur, jusqu'à ce que des anneaux d'interférence
puissent être observés sur l'écran.
3. Puis insérer le filtre jaune dans le porte-lentille et éteindre la lumière de la pièce. En tournant les
trois vis de réglage sur l'appareil des anneaux de Newton, la lentille plan-convexe est réglée sur
la plaque de verre à face parallèle de sorte que le centre lumineux des anneaux d'interférence
est dans le point médian de l'échelle millimétrique projetée sur l'écran. En faisant ce réglage,
Assurez-vous que la lentille et la plaque de verre ne font que toucher. Ceci est accompli quand
on n’a plus des anneaux qui émergent du centre de l'anneau lorsque les vis de réglage sont
serrées.

5
4. Remplir le tableau suivant pour le filtre jaune
n
1
2
3
4
5
6
7
8
9
10
r (mm)
r
2
(mm
2
)
5. Tracer le graphe de r2 en fonction de n pour le filtre jaune
6. Calculer la pente de la droite par la méthode des moindres carrées
7. à partir de la relation 4, calculer jaune pour R=12,141 m
8. Répéter ces mesures pour les deux autres filtres (vert et bleu)
9. Tracer sur le même graphique tous les droites r2 en fonction de n
10. Calculer vert et bleu pour R=12,141 m
11. Comparer et conclure
12. La pente des droites étant déjà calculée pour les différents filtres et étant donné la longueur
d'onde λ pour chaque filtre, calculer une valeur moyenne de R le rayon de courbure de la lentille
plan-convexe
13. Calculer une erreur sur R
Remarque
Dans la configuration décrite, les anneaux de Newton sont observés en lumière transmise. Les anneaux
d'interférence sont complémentaires de ceux de la lumière réfléchie. Dans le dernier cas, par
conséquent, les anneaux de lumière sont comptés et pas les sombres.