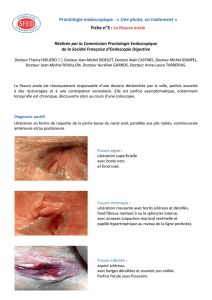
Mécanique de la rupture

Mécanique de la rupture
La mécanique de la rupture tend à définir une propriété du matériau qui peut se traduire par sa résistance
à la rupture fragile (fracture) ou ductile. Car si les structures sont calculées pour que les contraintes
nominales ne dépassent pas, en règle générale, la limite d'élasticité du matériau et soient donc par voie
de conséquence à l'abri de la ruine par rupture de type ductile ; elles ne sont pas systématiquement à
l'abri d'une ruine par rupture de type fragile, que ce soit à partir d'une fissure préexistante à la mise en
service ou créée en service par fatigue ou par corrosion sous contrainte.
Modes de propagation d'une fissure
La propagation d'une fissure dans un volume peut se décomposer en 3 composantes appelées mode :
 Mode I - Ouverture selon la normale au plan de la fissure,
 Mode II - Ouverture parallèlement au plan de la fissure et perpendiculaire au front de fissure, et
 Mode III - Ouverture parallèlement au plan de la fissure et parallèlement au front de fissure.
Chaque mode est généralement caractérisé individuellement bien que la propagation réelle d'une fissure
soit la combinaison de ces 3 modes.
Figure 1. Illustration des trois modes de propagation d'une fissure.
Mode de rupture fragile
Le mode de rupture de type fragile peut survenir quand les sollicitations ont lieu dans les circonstances
suivantes :
 Basses températures,
 Grandes vitesses de chargement, et
 Défauts préexistants ou créés pendant le service.
Les ruptures brutales dont il s'agit peuvent être classées en deux catégories :
 Les ruptures fragiles liées à l'absence de ductilité du matériau sollicité sous une certaine température
(Température de paroi minimum admissible) comme les aciers doux, et
 Les ruptures ductiles sans prévenir, c'est-à-dire à très faible déformation plastique. Ce peut être le
cas pour des matériaux à haute limite d'élasticité où il n'existe pas de dépendance très nette entre la
ténacité et la température c'est-à-dire où la rupture en charge est liée à la propagation quasi
instantanée d'une fissure à partir d'un défaut préexistant.
Les essais classiques de ténacité (essais de résilience par exemple) ne permettent pas de définir une
grandeur susceptible de prendre en compte le phénomène de rupture de type fragile dans les calculs.

Ce qui suit explique le concept de résistance ou d'endurance à la fracture, ainsi que les paramètres
auxquels il est assujetti comme la température, le taux de déformation, la concentration de contraintes
ou encore le niveau de contrainte.
Des méthodes d'examen et d'essai mises à disposition des concepteurs pour apprécier l'aptitude à la
rupture fragile sont présentées, ainsi qu'une approche de la mécanique linéaire élastique de rupture.
Dans la conception de structures en matériaux ductiles, l'aptitude à résister à la charge de manière
sécurisée est basée sur l'analyse des contraintes de façon à assurer que la contrainte nominale reste
confinée dans le domaine élastique du matériau. Des ruptures qui surviennent à l'intérieur de ce domaine
élastique (en deçà de la limite d'élasticité du matériau) sont classées comme ruptures fragiles. Ces
ruptures peuvent s'initier à partir de petits défauts de continuité au sein du matériau (ligne d'inclusions
intermétalliques par exemple) ou de défauts de type fissure qui n'altèrent pas grandement la distribution
de la contrainte nominale et qui ne sont habituellement pas pris en considération dans l'analyse de
contrainte.
Pour un taux de chargement très élevé, une discontinuité peut fortement diminuer la bonne ductilité du
matériau prédite par un essai de traction satisfaisant réalisé sur éprouvettes usinées (sans défaut de
surface et aux contours arrondis) et provoquer la ruine de la structure par rupture fragile. C'est ce mode
de rupture qui est à l'origine du tragique accident survenu à la plateforme pentagone Alexander Kielland.
Il devient par conséquent évident qu'une conception saine doit bannir toutes les discontinuités
(singularités), ce qui reste difficile en construction soudée et surtout en construction moulée.
Pour beaucoup de structures traditionnelles comme les bateaux, les ponts et les équipements sous
pression, l'expérience de la conception, des matériaux et des modes de fabrication ont permis d'établir
une corrélation satisfaisante, pour le matériau, entre réussite à l'essai de flexion par choc standard sur
éprouvette entaillée et bonne tenue en service.
Dans le domaine aéronautique, l'analyse de fatigue permet souvent de prévoir la durée de vie à
l'amorçage des fissures. On utilise donc la phase de propagation de fissure pour réaliser des inspections
en prévention de la rupture dont les intervalles sont définis par la mécanique de la rupture.
Une des motivations en faveur de l'application des concepts de la mécanique de la rupture et des essais
à réaliser sur joints soudés ou pièces moulées est d'être en mesure de se prémunir, dès la phase de
conception, des effets produits par les discontinuités présentes. Il est largement reconnu que les joints
soudés et les pièces moulées comportent toujours un certain nombre de discontinuités, ce qui place le
concepteur devant un dilemme. Le concepteur souhaitera toujours utiliser des joints soudés ou des pièces
moulées exempts de discontinuités, ce qui n'est absolument pas réaliste.
L'approche pratique consiste à reconnaître la présence de ces discontinuités au sein des assemblages et
de déterminer une taille critique à partir de laquelle une discontinuité devient préjudiciable, autrement
dit à partir de laquelle il faut les rechercher et les éliminer. Mais comment décider à partir de quelle
dimension critique une discontinuité a toutes les probabilités de devenir préjudiciable ?
Étant donné que la méthode conventionnelle d'essai de flexion par choc n'est plus appropriée, les
méthodes d'essais issues de la mécanique de la rupture (essais de fracture), lorsqu'ils sont applicables,
peuvent contribuer à établir une corrélation entre taille critique d'une discontinuité et contrainte de
rupture pour un matériau ou une soudure donné et donc permettre une estimation directe de la taille des
défauts acceptables pour différentes configurations et conditions de fonctionnement. Cependant,
l'évolution permanente des matériaux (matériaux à haute limite d'élasticité), les conceptions de plus en
plus complexes et les nouvelles technologies de soudage ou de moulage font que les ingénieries ne
peuvent pas avoir le recul nécessaire sur le comportement de ces nouvelles conceptions et les contraintes
attendues pas forcément attestées. En conséquence il y aura toujours une grande nécessité, pour le
concepteur, à traiter de manière analytique le problème des discontinuités.

L'idée de Griffith
La mécanique de la rupture a été inventée pendant la Première Guerre mondiale par l'ingénieur
aéronautique anglais, A. A. Griffith, pour expliquer la rupture des matériaux fragiles1. Le travail de
Griffith a été motivé par deux faits contradictoires :
 la contrainte nécessaire pour rompre un verre courant est d'environ 100 MPa ;
 la contrainte théorique nécessaire à la rupture de liaisons atomiques est d'environ 10 000 MPa.
Une théorie était nécessaire pour concilier ces observations contradictoires. En outre, les
expérimentations sur les fibres de verre que Griffith lui-même a mené suggèrent que la contrainte de
rupture augmente d'autant plus que le diamètre des fibres est petit. Par conséquent il en déduit que le
paramètre de résistance uniaxiale à la rupture Rr, utilisé jusqu'alors pour prédire les modes de défaillance
dans le calcul des structures, ne pourrait pas être une valeur indépendante des propriétés du matériau.
Griffith suggère que la faiblesse de la résistance à la rupture observée dans ses expériences, ainsi que la
dépendance de l'intensité de cette résistance, étaient due à la présence de défauts microscopiques
préexistant dans le matériau courant.
Pour vérifier l'hypothèse de défauts préexistants, Griffith a introduit une discontinuité artificielle dans
ses échantillons expérimentaux. La discontinuité artificielle était une forme de fissure débouchante plus
importante que les autres discontinuités supposées préexistantes dans l'échantillon.
Les expériences ont montré que le produit de la racine carrée de la longueur de défauts (a) et la contrainte
à la rupture (σf) était à peu près constante, ce qui est exprimé par l'équation :
figure 2. Fissure débouchante dans une éprouvette chargée en mode I.
Critère de Griffith : calcul simplifié
Si l'on suppose la présence d'une fissure de taille « a » dans un matériau sous traction (contrainte σ), le
calcul de la valeur σf de la contrainte à partir de laquelle cette fissure grandit peut s'estimer simplement.
L'explication de cette relation en termes de théorie de l'élasticité linéaire pose un problème de point
singulier. En élasticité linéaire, la théorie prédit que la contrainte (et par conséquent l'effort) à l'extrémité
d'une fissure dans un matériau idéalement élastique est infinie. Pour éviter ce problème, Griffith a
développé une approche thermodynamique pour expliquer la relation qu'il a observée.

Le développement d'une fissure nécessite la création de deux nouvelles surfaces et donc une
augmentation de l'énergie de surface. Griffith a trouvé une expression pour la constante C sur le plan de
l'énergie de surface de la fissure en résolvant le problème de l'élasticité d'une fissure finie dans une
plaque élastique. En bref, l'approche était la suivante :
 Calculer l'énergie potentielle stockée dans un échantillon parfait sous une charge de traction
uniaxiale,
 Ajuster la contrainte de sorte que la charge appliquée ne déforme pas (plastiquement ?)
l'échantillon, puis introduction d'une fissure dans l'éprouvette. La fissure relaxe la contrainte et, par
voie de conséquence, relaxe l'énergie élastique aux abords des faces de la fissure. D'autre part, de
par son existence, la fissure augmente l'énergie de surface totale de l'échantillon.
 Calculer la différence d'énergie libre (énergie de surface - énergie élastique) en fonction de la
longueur de la fissure. La rupture se produit lorsque l'énergie libre atteint une valeur maximale
pour une longueur critique de fissure, au-delà de laquelle l'énergie libre diminue du fait de la
propagation de la fissure (augmentation de l'énergie de surface) c'est-à-dire de l'augmentation
de la longueur de la fissure jusqu'à provoquer la rupture. Grâce à cette méthode, Griffith a
constaté que :
Où : E est le module de Young du matériau, et
γ est la densité d'énergie de surface du matériau
Les valeurs E = 62 GPa et γ = 1 J/m2 donnent un excellent modèle pour déterminer la contrainte de
rupture prédite par Griffith pour un matériau fragile.
Apports de G. R. Irwin
La théorie de Griffith concorde parfaitement avec les données expérimentales sur des matériaux
très fragiles tels que le verre. Pour des matériaux ductiles tels que l'acier, bien que la
relation soit toujours valable, l'énergie de surface (γ) prédite par la théorie de Griffith est
souvent irréaliste. Un groupe de travail dirigé par G. R. Irwin3 à l'US Naval Research Laboratory (NRL),
constitué durant la Seconde Guerre mondiale, a réalisé que la plasticité doit jouer un rôle important dans
la rupture des matériaux ductiles.
Dans les matériaux ductiles (et même dans des matériaux qui semblent être fragiles), une zone
plastique se développe en front de fissure. L'augmentation de la dimension de la zone plastique est
fonction de l'augmentation de la charge jusqu'à ce que la fissure se propage libérant les contraintes en
arrière du fond de fissure. Le cycle de chargement/libération de chargement plastique aux abords du
front de fissure conduit à la dissipation d'énergie comme le ferait un traitement thermique de relaxation
de contrainte. Par conséquent, un terme dissipatif doit être ajouté à la relation de l'équilibre énergétique
tel qu'élaboré par Griffith pour les matériaux cassants. En termes physiques, de l'énergie supplémentaire
est nécessaire pour que la propagation des fissures se produise dans les matériaux ductiles si on les
compare aux matériaux fragiles.
La stratégie d'Irwin était de partitionner l'énergie :
 L'énergie stockée en déformation élastique (effet ressort) qui se libère lors de la propagation d'une
fissure. Telle est la force motrice thermodynamique de rupture.
 L'énergie dissipée qui comprend la dissipation plastique et l'énergie de création de surface (et toutes
les autres forces dissipatives qui peuvent être au travail). L'énergie thermodynamique dissipée
fournit une résistance à la rupture. L'énergie totale dissipée est donnée par :

où Ɣ est l'énergie de surface et Gp est la dissipation plastique (ainsi que la dissipation provenant
d'autres sources) par unité de surface de la fissure.
La version modifiée du critère énergétique de Griffith peut alors être écrite comme :
 Pour un matériau fragile comme le verre par exemple, le terme d'énergie de surface domine
et .
 Pour un matériau ductile comme l'acier par exemple, le terme de dissipation plastique domine
et .
 Pour les plastiques polymères proches de la température de transition de phase de vitrification,
nous avons une valeur intermédiaire de .