Operateurs

OUAAQIL MOSTAFA
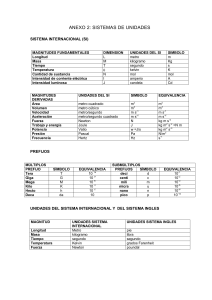
I - Coordonnées Cartesiennes :
II - Coordonnées Cylindriques :
x
y
z
x
y
z
M
o
i
j
k
o
M
dx
dy
dz
x
y
z
M
o
θ
r
e
e
z
e
x
y
z
M
o
θ
dr
rdθ
dz
r
z
kAjAiA
zA yA xA
A
zf yf xf
f
k
y
A
x
A
j
x
A
z
A
i
z
A
y
A
AArot
z
A
y
A
x
A
AAdiv
k
z
f
j
y
f
i
x
f
ffgrad
dzdydxdV
kdzjdyidxOMdrd
kzjyixOMr
zyx
x
y
z
x
y
z
z
y
x
...
...
.
....
..
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
11
.
1
..
1
11
.
..
1
..
sin ...
cos ..
zff r
r
f
r
rr
f
e
A
Ar
rr
e
r
A
z
A
e
z
A
A
r
AArot
z
A
A
r
Ar
rr
AAdiv
e
z
f
e
f
r
e
r
f
ffgrad
dzddrrdV
ryedzerdedrOMdrd
rxezerOMr
z
rzr
r
z
z
r
zr
zr
zr

OUAAQIL MOSTAFA
(V)
(S) surface fermée
entourant le volume (V)
(C)
(S)
dS
dl
(S) surface s’appuyant
sur le contour (C)
III - Coordonnées Sphériques :
x
y
z
M
r
e
e
e
o
θ
φ
r
x
y
z
M
o
dφ
dθ
dr
r sinθdφ
r dθ
2
2
2222
2
2
2
2
sin
1
sin
sin
11
.
1
.
sin
11
.sin
sin
1
sin
1
sin
sin
11
.
.
sin
1
.
1
..
cos sin
sinsin .sin..
cossin .
f
r
f
r
fr
r
r
f
e
A
Ar
rr
eAr
r
A
r
e
A
A
r
AArot
A
r
A
r
Ar
r
r
AAdiv
e
f
r
e
f
r
e
r
f
ffgrad
rzdddrrdV
ryedredredrOMdrd
rxerOMr
r
r
r
r
r
r
r
)( )(
)( )(
)( )(
2
.
...
..
2
1
0
0
S V
S V
C S
(C) (S)
(S) (V)
zyx
dVAAdS
dVfgraddSf
fdSdlf
dS.Adl.A
.dVAdivdS.A
C.A.BB.A.CCBA
ArotAAgradA.grad.A
B.grad.AA.grad.BArotBBrotAB.Agrad
z
A
.B
y
A
.B
x
A
.BA.grad.Bavec
B.grad.AA.grad.BB.AdivA.BdivBArot
Brot.AArot.BBAdiv
Arotf.AfgradAf.rot
Af.divfgrad.AAf.div
fgradg.ggradf.f.ggrad
AAdivgradArotrot Arotdiv
ffgraddiv fgradrot
:lrotationneduFormule
:gradientduFormule
:KelvindeFormule
:Ampère-Stoxde Théorème
:kyOstrogradsGreende Théorème
12)
11)
10)
9)
8)
7)
6)
5)
4)2)
3)1)