cours-codage des images

C1.2- CODAGE ET CHIFFRAGE LYCEE BELLEVUE
Fabien Hospital
1/13
COURS 1 : CODAGE ET CHIFFRAGE DES IMAGES
1. REVISIONS CODAGE ..................................................................................................................................... 1
1.1. Les nombres entiers naturels ..................................................................................... 1
1.2. Les nombres rationnels ............................................................................................. 2
2. IMAGES ............................................................................................................................................................. 3
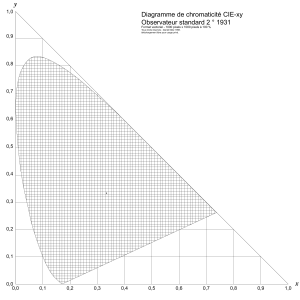
2.1. Notions de colorimétrie ............................................................................................. 3
2.2. Le modèle matriciel « bitmap »................................................................................. 4
2.3. Le format BMP ......................................................................................................... 5
2.4. Passer en niveau de gris ............................................................................................ 8
2.5. Image monochrome ................................................................................................... 8
3. LA COMPRESSION DES IMAGES « BITMAP » ........................................................................................ 9
3.1. Méthode à base de redondances : la compression RLE (Run-lenght encoding) ....... 9
3.2. Méthode à base de dictionnaire : La compression LZW (Lempel Ziv Welch) ....... 10
3.3. Méthode statistique : La méthode de Huffman ....................................................... 11
3.4. La compression avec pertes JPEG .......................................................................... 13
1. REVISIONS CODAGE
Un code binaire est une correspondance arbitraire entre un ensemble de symboles (0 et 1) et un ensemble
d’objets (chiffres, lettres, couleurs, etc.).
On appelle « octet (o) », un mot binaire de 8 bits.
Préfixes binaires (préfixes CEI)
Nom
Symb.
Facteur
kibi
Ki
210 = 1 024
mébi
Mi
220 = 1 048 576
gibi
Gi
230 = 1 073 741 824
tébi
Ti
240 = 1 099 511 627 776
pébi
Pi
250 = 1 125 899 906 842 624
Préfixes décimaux (préfixes SI)
Nom
Symb.
Facteur
Err.
kilo
k
103 = 1 000
2 %
méga
M
106 = 1 000 000
5 %
giga
G
109 = 1 000 000 000
7 %
téra
T
1012 = 1 000 000 000 000
10 %
péta
P
1015 = 1 000 000 000 000 000
13 %
Dans ce deuxième tableau, l’erreur indiquée dans la colonne de droite est celle effectuée quand on utilise un
préfixe SI à la place d’un préfixe binaire. L’usage de cette norme ne s’est pas encore généralisé. Microsoft
Windows continue à utiliser à tort les préfixes SI : par exemple 1 ko = 1024 octets au lieu de 1000 octets. D’autres,
comme les systèmes d’exploitation libres de type GNU/Linux, adoptent les préfixes binaires.
1.1. Les nombres entiers naturels
Le Code Binaire Naturel
Les codes utilisés en général pour représenter des nombres sont des codes pondérés : dans une base de
travail donnée, la valeur d’un rang donné, est un multiple par la base de celle du rang inférieur. Chaque
position de chiffre a un poids. Par exemple, pour un mot binaire à 8 bits (octet) :
0
1
1
0
1
0
0
1
Bit de poids fort (MSB)
Bit de poids faible (LSB)
Poids respectifs  27 26 25 24 23 22 21 20
On appelle ce codage à champ fixe car le nombre « k » de bits destinés au codage est constant. Il est
alors possible de représenter un entier naturel « N » tel que 0 N 2k-1.

C1.2- CODAGE ET CHIFFRAGE LYCEE BELLEVUE
Fabien Hospital
2/13
Un entier naturel codé sur un octet est forcément compris entre 0 et 255.
L’ Hexadécimal
Le système hexadécimal est un système de numération positionnel en base 16.
Il utilise ainsi 16 symboles, en général les chiffres arabes pour les dix
premiers chiffres et les lettres A à F pour les six suivants.
Le système hexadécimal est utilisé notamment en électronique numérique et
n informatique
1.2. Les nombres rationnels
Virgule flottante (« floating point ») le standard IEEE 754
On représente les nombres sous la forme : N = ± 1,M × BE
B : la base est 2
M : la mantisse
E : l’exposant
Le nombre à représenter, une fois traduit en binaire, peut toujours s’écrire sous la forme 1, ... ; ainsi il est
inutile de représenter ce premier 1 et on codera la mantisse à partir du bit suivant la virgule.
Les deux normes suivantes sont définies :
- IEEE 754 simple précision : sur 32 bits
SM : 1 bit ; Eb : 8 bits ; M : 23 bits (biais = 127)
- IEEE 754 double précision : sur 64 bits
SM : 1 bit ; Eb : 11 bits ; M : 52 bits (biais = 1023)
Exemple : Nous voulons représenter 525,5 au format IEEE 754 simple précision.
On commence par écrire 525,5 en base 2 : 525,5(10) = 1000001101,1(2)
On en déduit 525,5(10)= 1,0000011011(2) × 29.
On a donc :
– SM = 0 car le nombre est positif
– Eb = E + 127 = 9 + 127 = 136(10) = 10001000(2) en base 2 sur 8 bits
– M = 00000110110000000000000(2)
La représentation du nombre 525,5 en binaire avec la norme IEEE 754 est donc :
0 10001000 00000110110000000000000(2) = 48036000(16)
En arithmétique à virgule flottante, on peut obtenir un résultat valable, ou alors rencontrer un
problème de dépassement par valeur supérieure (overflow) lorsque le résultat est trop grand pour
pouvoir être représenté, ou par valeur inférieure (underflow) lorsque le résultat est trop petit.
Certaines représentations sont réservées à la représentation de l’infini ou de codes d’erreurs. Ce qui
a été dit précédemment est valable pour tous les nombres dont la représentation au format IEEE 754,
a un exposant biaisé Eb strictement compris entre 0 et Valeur Max (255 en simple précision et 2047
en double précision).

C1.2- CODAGE ET CHIFFRAGE LYCEE BELLEVUE
Fabien Hospital
3/13
2. IMAGES
Problème : Un ordinateur traite de l’information sous forme numérique binaire. Comment
coder les images à l’aide de codes binaires ?
Il existe deux modes de codage d’une image numérique :
1. Le mode matriciel (« bitmap ») : il repose sur le principe d’une grille de pixels,
2. Le mode vectoriel (« vector ») : on décrit les propriétés mathématiques des formes
de l’image.
On s’intéresse par la suite au codage des images par le mode matriciel.
2.1. Notions de colorimétrie
Problème : Comment coder les couleurs à l’aide de codes binaires ?
La synthèse additive est utilisée par les moniteurs et les projecteurs. Elle est constituée des trois lumières
de base qui sont le Rouge, le Vert et le Bleu (RVB). Les couleurs secondaires sont plus claires que les
primaires, c’est pour cela que leur synthèse est appelée additive.
La synthèse soustractive est utilisée
dans l’imprimerie et par les
imprimantes. Les couleurs primaires
sont le Cyan, le Magenta, le Jaune et le
Noir (CMJN). Si on mélange deux
couleurs primaires, le résultat sera une
couleur secondaire plus sombre qui
absorbera donc plus de lumière, c’est
pour cette raison que cette synthèse est
nommée soustractive.
Un modèle de colorimétrie est une manière
de coder des couleurs avec des nombres.
Le modèle Lab caractérise une couleur avec :
 un paramètre d'intensité correspondant à la luminance : la combinaison L* est la clarté, elle va de
0% (noir) à 100% (blanc),
 deux paramètres de chrominance qui décrivent la couleur : la composante
a* représente la gamme de l'axe du vert (-128) au rouge (+128). La
composante b* représente la gamme de l'axe du bleu (-128) au jaune
(+128). Ce modèle est proche de la vision humaine.
Le modèle RVB caractérise une couleur à l'aide de trois paramètres (chacun sur
un octet, soit un nombre de 0 à 255) correspondant aux trois couleurs Rouge, Vert
et Bleu.
00 00 00(16) = (0,0,0) = noir
Une image vectorielle peut être zoomée sans que cela n’altère
la qualité du rendu. Ce mode est adapté aux formes et images
qui ne sont pas trop complexes : logos, typographie, plans,
cartes, etc. Les formats de fichiers vectoriels sont PostScript,
PDF, SVG, etc.
Le nombre de pixels utilisés par unité de longueur donne un
rendu plus ou moins précis des formes de l’image. Un zoom
trop important fait apparaître la pixellisation de l’image. Les
formats de fichiers matriciels sont BMP, GIF, PNG, JPEG, etc.
Palette
« Paint
Shop »
Synthèse
soustractive
Synthèse
additive

C1.2- CODAGE ET CHIFFRAGE LYCEE BELLEVUE
Fabien Hospital
4/13
FF FF FF(16) = (255,255,255) = blanc
FF 00 00(16) = (255,0,0) = rouge
2.2. Le modèle matriciel « bitmap »
Une matrice de pixels (« picture elements ») est constituée d'un ensemble de points pour former une
image. Le pixel représente ainsi le plus petit élément constitutif d'une image numérique.
- Formats limités à 256 couleurs : GIF, PCX, PGM, etc.
- Formats acceptant différentes quantifications BMP, TIFF, TGA, PNG, etc.
- Formats limités à 16 millions de couleurs JPEG, etc.
Les images peuvent facilement être créées et stockées dans un tableau de pixels, la lecture et l’écriture
d’un pixel sont aisées.
Par contre, les fichiers peuvent être très gros (nécessité de compression).
De plus, il y a des problèmes de changement d'échelle (apparition d’effets de marches d’escalier ou de
flou avec interpolation). Enfin, les dimensions de l’image doivent être prévues pour la
résolution de l'interface de sortie (écran, imprimante).
La discrétisation d’une image se caractérise par sa définition, c'est-à-dire le nombre de pixels
utilisés.
La résolution de l’image établit un lien entre le nombre de pixels d’une image et sa taille
réelle. Elle se caractérise par un nombre de pixels par unité de longueur.
La quantification des couleurs est exprimée en bits par pixel (bpp) : 1 (deux
couleurs : noir et blanc par exemple), 8 (niveaux de gris entre 0 et 255 par exemple,
256 couleurs), 16 bits, etc
Exemple 1 :
« 800 600 » signifie une largeur de 800 et une hauteur de 600 pixels.
« 600 dpi » (« ppp » : point par pouce, « dpi » : dots per inch) signifie 600 pixels par pouce (1 pouce =
25,4 mm).
En connaissant le nombre de pixels d'une image et la mémoire
nécessaire à l'affichage d'un pixel, il est alors possible de définir
exactement la taille qu’occupe le fichier.
Une définition du type 800 600 avec un codage sur 24 bits (3 octets)
des couleurs, donne un fichier image de taille 1,44 Mo.
8 dpi
25,4 mm
Pixel ?
En-tête (« header »)
Identificateur du format
Palette de couleur (éventuellement)
Données d’image
Suite de pixels éventuellement

C1.2- CODAGE ET CHIFFRAGE LYCEE BELLEVUE
Fabien Hospital
5/13
2.3. Le format BMP