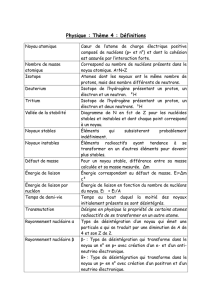
T STI2D - Santé Prévention et soin Chap. 11
Exercices
Radioactivité Correction des exercices
Données : c =3,00 x 108m.s-1 ; h=6,63 10-34 J.s ; 1eV → 1,6 10-19J
Exercice 1 : Le polonium
Marie et Pierre Curie ont découvert le polonium 210, 𝑃𝑜
, en 1898. Ce nucléide radioactif est un
émetteur alpha.
1. Donner la composition et la notation symbolique d'une particule α.
Une particule α est un noyau d’hélium composé de 2 protons et de 2 neutrons de symbole : 𝐻𝑒
.
2. De combien de protons et de nucléons sera constitué le noyau fils résultant de la désintégration
du polonium 210 ? Rechercher dans le tableau périodique le nom de ce nucléide et donner sa
notation.
Lois de conservation :
- Du nombre de nucléons : 210 = 𝐴 + 4 donc 𝐴 = 210 − 4 = 206
- Du nombre de charge : 84 = 𝑍 + 2 donc 𝑍 = 84 − 2 = 82
D’après le tableau périodique le noyau fils est un noyau de plomb : 𝑃𝑏
Exercice 2 :
On considère les trois nucléides suivants :
Le bore 12 ( 𝐵
), le carbone 12 ( 𝐶
), l'azote 12 ( 𝑁
).
Le noyau du carbone 12 est stable. Par contre les noyaux du bore 12 et de l'azote 12 sont instables et
radioactifs 𝛽.
1. Donner la composition du carbone 12.
Le carbone 12 est composé de Z=6 protons et de 12-6=6 neutrons.
2. Le bore 12, le carbone 12 et l'azote 12 sont-ils isotopes ? Justifier la réponse.
Des atomes isotopes ont le même nombre de protons Z, ici ces trois éléments ont un numéro atomique
(Z) différents, ce ne sont donc pas des isotopes mais 3 éléments chimiques différents.
3. Ecrire l’équation de désintégration du bore 12 en carbone 12. Quelle est la particule émise ?
Lois de conservation :
- Du nombre de nucléons : 12 = 12 + 𝐴 donc A= 12 − 12 = 0
- Du nombre de charge : 5 = 6 + 𝑍 donc 𝑍 = 5 − 6 = −1
La particule émise est donc un électron de symbole 𝑒
Equation de désintégration : 𝐵
→ 𝐶
+ 𝑒
4. Lors de la désintégration du bore 12 en carbone 12, un nucléon change de nature. S'agit-il
d'un neutron ou d'un proton ?
La particule qui change de nature est un neutron qui devient un proton.

T STI2D - Santé Prévention et soin Chap. 11
Exercices
Radioactivité Correction des exercices
Exercice 3 : Radioactivité de l’iode
Lors de la catastrophe de Tchernobyl, de nombreux corps radioactifs ont été rejetés dans l’atmosphère, en
particulier de l’iode 131 qui est émetteur 𝛽 et 𝛾 (demi-vie = 8 jours).
1. Ecrire l’équation de cette désintégration radioactive.
La particule émise est un électron 𝑒
et d’après le tableau période le numéro atomique de l’iode est
53
Lois de conservation :
- Du nombre de nucléons : 131 = 𝐴 + 0 donc 𝐴 = 131
- Du nombre de charge : 53 = 𝑍 − 1 donc 𝑍 = 53 + 1 = 54
D’après le tableau périodique le noyau fils est un noyau de xénon: 𝑋𝑒
𝐼
→ 𝑋𝑒
+ 𝑒
2. L’iode 131 déposé par le nuage radioactif peut ensuite être ingéré sous forme d’aliment. Dans
l’organisme, l’iode se fixe préférentiellement sur la thyroïde.
2.1. Pourquoi la radioactivité est-elle dangereuse pour les organismes vivants ?
Pour les êtres vivants, la radioactivité est dangereuse car elle irradie les cellules et l’ADN et peut provoquer
un dérèglement et l’apparition de cancer.
2.2. Pour la protection des populations, il est prévu de distribuer, en cas d’accident nucléaire, des
comprimés contenant un isotope non radioactif de l’iode. Quel est l’intérêt de cette mesure de
protection ?
L’iode se fixe sur la tyroïde dans le corps humain, lors d’un accident radioactif cet iode est radioactif,
on donne des comprimés à base d’iode non radioactif afin qu’ils se fixent dans la tyroïde avant les
noyaux radioactifs.

T STI2D - Santé Prévention et soin Chap. 11
Exercices
Radioactivité Correction des exercices
Exercice 4 : Radiothérapie
1. Donner la composition du noyau d’iridium.
Le noyau d’iridium 𝐼𝑟
est composé de Z=77 protons et de 192-77=115 neutrons.
2. Quelle est la particule émise lors d’une désintégration 𝛽 ?
La particule émise est un électron 𝑒
3. Écrire l’équation de désintégration du noyau d’iridium 192 sachant que le noyau fils est le
platine Pt.
D’après le tableau période le numéro atomique du platine est 78
Lois de conservation :
- Du nombre de nucléons : 192 = 𝐴 + 𝐴
- Du nombre de charge : 77 = 78 + 𝑍 donc 𝑍 = 77 − 78 = −1
La particule émise est un électron 𝑒
donc 𝐴 = 192 − 0 = 192
𝐼𝑟
→ 𝑃𝑡
+ 𝑒
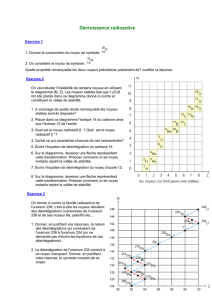
4. À l’aide de la courbe de décroissance radioactive, déterminer la demi-vie T de l’iridium 192.
5. Sachant que Δ𝐴 = 1,0 𝑀𝐵𝑞 𝑒𝑡 𝐴 = 15 𝑀𝐵𝑞, calculer l’incertitude Δ𝑡 et exprimer la période T
avec son incertitude.
∆𝑡 = ∆
. et 𝜆 =
=
= 9,24. 10 𝑗𝑜𝑢𝑟 donc ∆𝑡 = ∆
. =,
×,. = 7 𝑗𝑜𝑢𝑟
Donc 𝑇 = 75 ± 7 𝑗𝑜𝑢𝑟𝑠
6. Quelle valeur le pourcentage de noyaux radioactifs restants au bout de 220 jours prend-il ?
Choisir parmi les propositions suivantes : 50%, 33%, 25% ou 10%, et justifier votre réponse.
= 2,9 ; 220 jours correspondent à environ 3 périodes, au bout d’une période, il reste 50% de
noyaux radioactifs, au bout de 2 périodes, il en reste
= 25 % et au bout de 3 périodes
= 12,5%.
Parmi les propositions précédentes, on choisit donc 10 %.
75
𝐴
2

T STI2D - Santé Prévention et soin Chap. 11
Exercices
Radioactivité Correction des exercices
Exercice 5 : Dose d’énergie absorbée
Une partie du rayonnement électromagnétique émis lors d’une désintégration peut être absorbée par
l’organisme humain.
La dose d’énergie absorbée D est égale à : 𝐷 =
Avec : E : énergie transférée en joules (J)
m : masse de matière irradiée (kg)
D : dose d’énergie absorbée
1. Citer l’unité de mesure de la dose d’énergie absorbée D.
La dose d’énergie absorbée D s’exprime en gray (Gy) soit des joules par kilogramme de matière irradiée.
2. Pour un litre de lait radioactif absorbé, un enfant de masse m = 10 kg reçoit une énergie
E = 0,0010 J. Calculer la dose d’énergie D absorbée par cet enfant.
𝐷 = 0,0010
10 = 1,0. 10 𝐺𝑦
3. Convertir cette énergie en électronvolt.
𝐸 = 1,0. 10
1,6. 10 = 6,25. 10𝑒𝑉
4. Calculer la fréquence puis la longueur d’onde de ce rayonnement.
𝐸 = ℎ. 𝜈 donc 𝜈 =
=,
,. = 1,5. 10 𝐻𝑧
𝐸 = .
donc 𝜆 = .
=,.×,.
, = 2,0. 10 𝑚
Exercice 6 : Le molybdène
La désintégration du molybdène 99 (émetteur 𝛽) donne comme noyau fils le technétium 99 qui se
trouve dans un état métastable (excité) : 𝑇𝑐
. Ce noyau se désexcite avec une période de 6h, en
émettant un rayonnement gamma d'énergie égale à 140 keV.
1. Quelle est la nature du rayonnement gamma ?
Le rayonnement gamma est un rayonnement électromagnétique, de très courte longueur d’onde constitué
de photons de grande énergie.
2. Donner l'équation de la désintégration du molybdène 99.
𝑇𝑐
∗→ 𝑇𝑐
+ 𝛾
3. Calculer la longueur d'onde dans le vide de ce rayonnement.
𝐸 = .
donc 𝜆 = .
=,.×,.
.×,. = 8,87. 10 𝑚

T STI2D - Santé Prévention et soin Chap. 11
Exercices
Radioactivité Correction des exercices
Exercice 7 : Radiothérapie cancereuse
Un organe cancéreux d'un patient est traité par radiothérapie. La prescription du médecin prévoit une
dose d'irradiation totale de l'organe 𝐷 = 50 𝐺𝑦 . Lors d'une séance de radiothérapie, l'organe de masse
𝑚 = 800 𝑔, est irradié pendant 10 min et chaque seconde il absorbe l'énergie de 1,4.10 photons 𝛾
environ. L'énergie de chaque photon est égale à 12 MeV.
1. Quel est le nombre N de photons γ qui irradient l'organe au cours d'une séance ? En déduire
l'énergie, en joule, absorbée par l'organe lors d'une séance.
𝑁 = 10 × 60 × 1,4.10= 8,4. 10 𝑝ℎ𝑜𝑡𝑜𝑛𝑠
𝐸 = 8,4. 10 × 12 = 1,0. 10 𝑀𝑒𝑉
2. Quelle est la dose absorbée par l'organe au cours d'une séance ? En déduire le nombre de
semaine de traitement du patient, si celui subit 5 séances par semaine.
𝐷 = 𝐸
𝑚=1,0. 10 × 10× 1,6. 10
0,800 = 2 𝐺𝑦
3. Quelles dispositions doivent être prise pour protéger le personnel soignant des risques d'une
exposition dangereuse aux radiations ?
Pour protéger le personnel soignant, celui-ci ne doit pas être présent dans la salle de radiothérapie au moment
de l’administration de la dose. De plus la salle doit être étanche aux radiations gamma. Pour cela on pose des
plaques de plomb sur les murs et on utilise des vitres d’observation spéciales contenant également du plomb.
On peut aussi contrôler à l’aide d’un dosimètre l’irradiation cumulée des personnels pour éviter tout risque
de dépassement de la dose limite.
Exercice 8 : Noyaux inconnus
Les deux radionucléides ont les mêmes périodes radioactives différentes, or chaque nucléide a sa
propre période. Ces deux radionucléides sont donc identiques.
 6
6
1
/
6
100%