Dynamique des rotors en torsion : Analyse des régimes

Toute reproduction sans autorisation du Centre français d’exploitation du droit de copie est strictement interdite.
© Techniques de l’Ingénieur, traité Génie mécanique BM 5 123 − 1
Dynamique des rotors en torsion
Analyse des régimes de fonctionnement
par Henri BLANC
Ingénieur des arts et métiers
Docteur ingénieur agrégé en mécanique
Professeur à l’Ensam Talence
et article met en œuvre les résultats de la modélisation des rotors en torsion
pour l’étude des régimes de fonctionnement permanents et transitoires qui
sont représentatifs des conditions réelles d’utilisation des lignes d’arbres. Les
trois analyses usuelles suivantes sont présentées : étude des vibrations libres,
étude des vibrations forcées et étude des régimes transitoires.
Cet article fait partie d’une série sur la dynamique des rotors en torsion :
— BM 5 120 Introduction ;
— BM 5 121Types d’excitations permanentes ;
— BM 5 122 Répartition de l’inertie et de la raideur ;
— BM 5 123 Analyse des régimes de fonctionnement ;
— BM 5 124 Étude des amortisseurs de torsion.
1. Vibrations libres....................................................................................... BM 5 123 - 2
1.1 Mise en équations ....................................................................................... — 2
1.2 Résolution numérique du système aux valeurs propres ......................... — 2
1.3 Exemple d’adaptation d’une ligne d’arbres .............................................. — 3
2. Vibrations forcées ................................................................................... — 5
2.1 Identification des paramètres d’amortissement ....................................... — 6
2.2 Définition de l’importance d’un harmonique du couple produit
par un système bielle-manivelle ................................................................ — 8
2.3 Mise en équations ....................................................................................... — 9
2.4 Méthode de résolution................................................................................ — 10
2.5 Résultats recherchés.................................................................................... — 10
2.6 Exemples...................................................................................................... — 11
3. Régimes transitoires ............................................................................... — 16
3.1 Caractérisation des régimes transitoires................................................... — 16
3.2 Expression du système différentiel............................................................ — 16
3.3 Résolution numérique................................................................................. — 16
3.4 Exemple........................................................................................................ — 17
Pour en savoir plus .......................................................................................... Doc. BM 5 125
C

DYNAMIQUE DES ROTORS EN TORSION ____________________________________________________________________________________________________
Toute reproduction sans autorisation du Centre français d’exploitation du droit de copie est strictement interdite.
BM 5 123 − 2© Techniques de l’Ingénieur, traité Génie mécanique
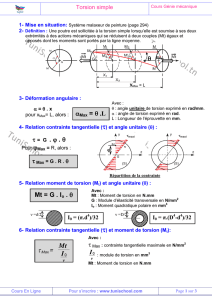
1. Vibrations libres
1.1 Mise en équations
Dans la majorité des cas (cf. [BM 5 122]), le modèle final obtenu
peut être représenté simplement comme l’assemblage de ressorts
de torsion sans masse dont on connaît la rigidité K et la connecti-
vité. Les extrémités de chacun d’eux sont liées à des disques d’iner-
tie indéformables dont on a identifié le moment d’inertie I. Le
paramétrage caractérise la position et la vitesse angulaire de chaque
disque du modèle. À partir des expressions de l’énergie cinétique et
de la fonction de force écrites en fonction des paramètres de vitesse
et de déplacement indépendants, le formalisme de Lagrange per-
met d’obtenir le système différentiel représentant les vibrations
libres de torsion.
Pour illustrer le propos, on se place dans le cas d’un modèle non
ramifié composé de
n disques (figure 1).
L’énergie cinétique
E
c et la fonction de force
U s’écrivent :
L’équation différentielle obtenue pour les paramètres α
i
, est :
Si
i = 1
Si 1 <
i < n
Si i = n
L’écriture du système différentiel sous forme matricielle conduit
à :
(1)
avec vecteur des accélérations ,
{α} vecteur des déplacements α
i
,
[
M ] matrice de masse diagonale (figure 2),
[
K ] matrice de rigidité symétrique (figure 3).
1.2 Résolution numérique du système
aux valeurs propres
On cherche des solutions non identiquement nulles représentant
à partir des conditions initiales données les vibrations possibles des
disques du modèle soumis à aucune excitation extérieure perma-
nente. Ces solutions sont de la forme :
{α} = {
a } cos ω t (2)
avec ω (rad/s) pulsation du mouvement libre.
En insérant ces solutions (2) dans le système différentiel (1), on
obtient le système aux valeurs propres suivant :
− ω2 [
M ]{ a } + [ K ]{ a } = 0
Les solutions obtenues définissent les pulsations propres ω
i
telles
que :
Pour chaque pulsation propre ω
i
, le vecteur propre associé {Φ
i
} est
déterminé. Il est solution du système linéaire :
Remarque
Dans la mesure où le modèle est ramifié, la démarche de mise
en équations reste identique. La matrice de rigidité [
K ] obtenue
n’est plus tridiagonale mais, dans tous les cas, elle reste symé-
trique.
E
c1
2
--- I
i
α
ú
i
2
i 1=
n
∑
=
U 1
2
---
K
i
α
i
α
i 1+
Ð()
2
i 1=
n 1Ð
∑
Ð=
α
ú
i
d
d
t
------∂
E
c
∂ α
ú
i
---------
∂
E
c
∂ α
i
---------
Ð∂
U
∂ α
i
--------=
I1
α
úú 1
K
1
α
1
K
1
α
2
Ð+0=
I
i
α
úú
i
K
i 1Ð
α
i 1Ð
Ð K
i 1Ð
K
i
+() α
i
K
i
α
i 1+
Ð+0=
I
n
α
úú
n
K
n 1Ð
α
n 1Ð
Ð K
n 1Ð
α
n
+0=
M [] α
úú
{}
K [] α {}+0=
α
úú
{}
α
úú
i
Figure 1 – Modèle torsionnel générique d’une ligne d’arbres
Figure 2 – Structure de la matrice de masse du modèle
de la figure 1
Figure 3 – Structure de la matrice de rigidité du modèle
de la figure 1
I1
K
1
KiKi
+1
Kn
–1
K
2
I2
α1α2α3α
i –1 α i +1 α n –1 α n
α
i
I3I
i –1 I i +1 I n –1 I n
I
i
Paramètres
de position
I1
I2
I
n
K
1–
K
1
– K
2
– Kn
–2 –
Kn
–1
Kn
–2 +
Kn
–1
– Kn
–1
Kn
–1
– K
1
– K
3
– K
2
K
1 +
K
2
K
2 +
K
3
det K []ω
i
2
M []Ð()0=
ω
i
2
Ð M [] K []+() Φ
i
{} 0=

____________________________________________________________________________________________________ DYNAMIQUE DES ROTORS EN TORSION
Toute reproduction sans autorisation du Centre français d’exploitation du droit de copie est strictement interdite.
© Techniques de l’Ingénieur, traité Génie mécanique BM 5 123 − 3
Il existe des logiciels standards permettant la résolution de tels
problèmes (cf. [Doc. BM 5 125]). Généralement, la mise en données
de ces logiciels est très conviviale. Les données manipulées se résu-
ment à la définition de la connectivité des ressorts de torsion puis de
l’inertie des disques et enfin de la rigidité des ressorts de torsion.
Usuellement, seules les premières pulsations propres – les plus
petites – et leurs vecteurs propres associés sont nécessaires en vue
de l’adaptation des lignes d’arbres.
La résolution numérique de ce système aux valeurs propres met
en œuvre en général la méthode d’itération sur sous espace [9] qui,
d’ailleurs, est utilisée de manière très standard dans les logiciels de
calcul par éléments finis. Cette méthode permet de traiter des systè-
mes de taille très élevée et elle est dédiée au calcul des premières
pulsations propres du système.
1.3 Exemple d’adaptation d’une ligne
d’arbres
1.3.1 Méthodologie de l’analyse
Comme nous l’avons montré, le modèle représentant l’installa-
tion étudiée permet le calcul des premières pulsations propres et
des déformées modales associées. Ces résultats permettent une
première prévision du comportement vibratoire de la ligne d’arbres
dans la mesure où, par ailleurs, un bilan des pulsations des excita-
tions extérieures a été réalisé. Pour toutes les vitesses de fonction-
nement, il s’agit de confronter d’une part, les valeurs des pulsations
propres trouvées et, d’autre part, les valeurs des pulsations des har-
moniques non négligeables des couples excitateurs. En cas d’éga-
lité avec une tolérance de plus ou moins 10 %, on est en présence
d’une vitesse dangereuse qui est égale à la vitesse assurant, pour
l’harmonique de l’excitation extérieure identifiée, l’égalité des pul-
sations à la tolérance près.
Quand elle fonctionne au voisinage d’une vitesse dangereuse,
l’installation est le siège d’un phénomène de résonance qui est, très
souvent, destructeur.
L’adaptation de la ligne d’arbres par rapport à ce niveau d’analyse,
consiste à modifier la répartition initiale des raideurs et (ou) des
inerties de sorte à déplacer hors de la plage de fonctionnement tout
ou une partie des vitesses dangereuses. Dans certains cas, d’autres
solutions sont nécessaires, elles sont décrites en [BM 5 124].
1.3.2 Choix de l’installation étudiée
On considère l’installation de production d’air comprimé
dont le modèle a été défini en [BM 5 122, § 8.1]. Le groupe compres-
seur (figure 4) tourne à un régime constant (425 tr/min). Au cours
d’une journée, on peut estimer à 1 h le temps de marche à vide du
compresseur au régime nominal. Après quelques centaines d’heu-
res de fonctionnement, les dents des engrenages présentent une
usure anormale sur chaque flanc. Comme nous allons le montrer,
cela est caractéristique, bien souvent, d’amplitudes vibratoires donc
de couples oscillatoires trop importants au régime de fonctionne-
ment sans charge. Une telle disposition ne permettant pas un fonc-
tionnement correct, il y a lieu d’en modifier certains éléments pour
obtenir un service acceptable.
1.3.3 Résultats de l’étude en vibrations libres
Les tableaux 1 et 2 récapitulent les données nécessaires
(cf. [BM 5 122, § 8.1]).
(0)
Remarques
Dans la mesure où l’ordre de multiplicité de la pulsation pro-
pre est égal à
m , il existe m vecteurs propres associés.
La justification mathématique de ces résultats [9], [10] est
déduite des propriétés des matrices [ K ] et [ M ] qui sont symétri-
ques, semi-définies et positives.
Remarque : dans quasiment tous les cas, une ligne d’arbres
possède une (ou des) vitesse(s) de rotation moyenne(s) non
nulle(s). La première pulsation propre trouvée est donc nulle,
elle correspond au mouvement de rotation de corps solide pour
chacun des rotors composant la ligne d’arbres. Figure 4 – Groupe compresseur
Tableau 1 – Valeurs numériques des moments d’inertie
des disques du modèle du groupe compresseur (figure 4)
Disque
noMoment d’inertie (N · m · s2)
1 8,25
2 8,25
3 549,5
4 2,75
5 20,07
6 3,52
7 3,52
8 116
Première
manivelle
Seconde
manivelle
Compresseur C
Paramètres
de position
Réducteur
RMoteur électrique M
VA
PV AGV
I1I2
K
1
K
2
K
3
K
4
K
5
K
6
K
7
I3I4I5I6I7I8
N
S0
α10 α20 α30 α40 α50 α60 α70 α80
(1)
(1)
(1) (1) (1)
(1) (1) (1)
(1) (1)
a schéma
b modèle torsionnel ramené à la vitesse
de rotation du compresseur
Roue
N
E0
N
S0

DYNAMIQUE DES ROTORS EN TORSION ____________________________________________________________________________________________________
Toute reproduction sans autorisation du Centre français d’exploitation du droit de copie est strictement interdite.
BM 5 123 − 4© Techniques de l’Ingénieur, traité Génie mécanique
(0)
(0)
Les longueurs équivalentes (tableau 2) ont été calculées pour un
diamètre équivalent de 180 mm avec un module de cisaillement
transversal équivalent de 8 300 daN/mm2.
Les quatre premières pulsations propres (ou modes propres) ont
été calculées (tableau 3) et on présente les déformées modales
associées (tableau 4 et figure 5).
1.3.4 Bilan des sources d’excitation
Le tableau 5 analyse la pulsation de chaque source potentielle
d’excitation vis-à-vis des vibrations de torsion. Dans la colonne
observation, on repère les vitesses dangereuses pour le groupe
compresseur et pour chacune d’elle, on indique la pulsation propre
concernée.
1.3.5 Adaptation de la ligne d’arbres
De manière générale, il est intéressant de réaliser une étude de la
sensibilité des valeurs de rigidités et de moments d’inerties sur les
pulsations propres intéressantes. Grâce aux logiciels de calcul (cf.
[Doc. BM 5 125]), cette analyse est très rapide d’autant qu’elle est
souvent automatisée. Malgré tout, il est possible d’énoncer quel-
ques règles générales.
1.3.5.1 Influence de la raideur des tronçons
sur les pulsations propres
La modification de la rigidité torsionnelle d’un tronçon n’a
d’influence notable sur les pulsations propres que lorsque ce tron-
çon subit une relativement grande déformation. Dans ce cas, il est,
en général, le siège d’un nœud de vibration. Pour déplacer une
vitesse dangereuse, il est donc inutile de modifier la rigidité torsion-
nelle des autres tronçons, ceux qui stockent une énergie potentielle
relativement faible.
(0)
Pour les premiers modes, les nœuds de vibration sont situés près
des disques à grand moment d’inertie ou dans les tronçons de faible
rigidité torsionnelle. Or, généralement, près des disques à grand
moment d’inertie (volants), sont montés les accouplements élasti-
ques de liaison. Les nœuds de vibration sont donc presque toujours
localisés dans les accouplements. Il est possible, en modifiant la
rigidité de l’accouplement, de changer la pulsation propre de la
ligne d’arbres. C’est évidemment, du fait de sa simplicité, la pre-
mière opération à envisager. D’ailleurs, et d’une façon générale, on
évite que le nœud de vibration du premier mode soit ailleurs que
dans l’accouplement. Si l’on respecte cette règle, le choix de la rigi-
dité torsionnelle de l’accouplement est facile. En effet, dans ce cas,
la pulsation propre varie sensiblement comme la racine carrée de la
rigidité torsionnelle du tronçon situé au nœud de vibration. Cette
propriété est d’autant plus valable que la part de l’énergie poten-
tielle du système vibrant stockée dans l’accouplement est grande.
Enfin, si cette modification n’est pas suffisante pour écarter tout
danger, on agit sur les inerties.
Tableau 2 – Connectivité et valeurs numériques
des rigidités des ressorts de torsion du modèle du groupe
compresseur (figure 4)
Ressort de
torsion
noConnectivité Rigidité
torsionnelle
(N · m/rad)
Longueur
équivalente
(mm)
1 1 2 3,3 x 107259
2 2 3 2,78 x 107307
3 3 4 3,6 x 1062 375
4 4 5 1,52 x 107561,3
5 5 6 5,86 x 107146
6 6 7 6,41 x 1061 335
7 7 8 4,59 x 107186,5
Tableau 3 – Pulsations propres ω
i
du modèle du groupe
compresseur (figure 4)
No du mode tr/min rad/s
1 1 276 133,6
2 5 690 595,6
3 11 237 1 176,2
4 25 899 2 710,8
Figure 5 – Déformée modale du premier mode du modèle
de la figure 4
Tableau 4 – Amplitudes relatives du modèle du groupe
compresseur (figure 4) pour les quatre premières
pulsations propres non nulles
Disque
no
Mode no 1
ω
1 =
133,6 rad/s
Mode no 2
ω
2 =
595,6 rad/s
Mode no 3
ω
3 =
1 176,2 rad/s
Mode no 4
ω
4 =
2 710,8 rad/s
11111
2 0,99 0,91 0,65 − 0,83
3 0,98 0,71 − 0,025 − 1,19
4− 1,78 − 39,29 − 0,002 1 113
5− 2,43 − 46,24 0,003 4 − 123,2
6− 2,58 − 42,43 0,003 3 − 191
7− 3,96 0,69 0,000 1 − 42
8− 4,14 6,69 − 0,000 2 2,39
Amplitude relative
des disques
12 3 45678
1
0,99 0,98
– 1,78 – 2,43 – 2,58
– 3,96 – 4,14
N° des disques
Nœud de vibration
ω1 = 133,6 rad/s

____________________________________________________________________________________________________ DYNAMIQUE DES ROTORS EN TORSION
Toute reproduction sans autorisation du Centre français d’exploitation du droit de copie est strictement interdite.
© Techniques de l’Ingénieur, traité Génie mécanique BM 5 123 − 5
(0)
1.3.5.2 Influence de l’inertie des tronçons sur les pulsations
propres
Il faut noter qu’une modification modérée du moment d’inertie
des disques situés de part et d’autre d’un nœud de vibration a très
peu d’influence sur la pulsation propre. En revanche, tout change-
ment du moment d’inertie d’un disque proche d’un ventre de la
déformée modale entraîne une modification notable de la pulsation
propre. Un tel disque possède une amplitude de vibration relative-
ment grande et stocke de ce fait une grande partie de l’énergie ciné-
tique du système vibrant.
Pour une installation comportant un moteur thermique, on choisit
l’inertie du volant voire la raideur de l’accouplement pour que le
nœud de vibration du premier mode soit dans l’accouplement et
non dans le vilebrequin. Dans la mesure où l’on n’a pas besoin de
mettre sur le vilebrequin un volant de régulation, on peut minimiser
le moment d’inertie de ce volant, à condition de placer un accouple-
ment souple et à fort taux d’amortissement (accouplement caout-
chouc) afin de limiter les oscillations de torsion surtout durant les
phases transitoires.
(0)
2. Vibrations forcées
L’objectif principal de ce paragraphe est la détermination des
amplitudes de vibration des disques du modèle pour des conditions
de fonctionnement permanentes, c’est-à-dire une vitesse constante
et des sollicitations périodiques établies. À partir des déformations
trouvées pour chaque ressort de torsion, il est possible de calculer
une estimation de l’amplitude des contraintes de cisaillement qui
existent dans les tronçons du rotor associés.
Le modèle choisi pour cette étude est déduit du modèle utilisé
pour l’étude en vibrations libres. Il est complété par la représenta-
tion des phénomènes d’amortissement présents dans l’installation.
On utilise aussi les amplitudes et les phases des excitations pério-
diques.
Tableau 5 – Bilan des sources d’excitation du groupe compresseur (figure 4)
Sources de l’excitation Vitesse de rotation
(tr/min) Harmonique à considérer
Pulsation
de l’harmonique
(tr/min)
Pulsation propre
correspondante
(tableau 3)Observations
Balourd arbre
compresseur 425 1 425 aucune pas de danger
Balourd arbre moteur 1 485 1 1 485 aucune pas de danger
Pignon réducteur 1 485 35 (nb. de dents ;
(cf. [BM 5 121, § 1, 2]) 51 975 aucune pas de danger
Roue réducteur 425 51 975 aucune pas de danger
Système bielle-manivelle 425
1 425 aucune pas de danger
2 850 aucune pas de danger
3 1 275 1 276 danger (1er mode)
4 1 700 aucune pas de danger
5 2 125 aucune pas de danger
6 2 550 aucune pas de danger
7 2 975 aucune pas de danger
8 3 400 aucune pas de danger
Moteur électrique 3 000 ............ 50 Hz ou 3 000 tr/min aucune pas de danger
Exemple : application au groupe compresseur
Le tableau 5 fait apparaître que, pour le premier mode, il y a réso-
nance avec l’harmonique d’ordre 3 du couple résistant dû aux systè-
mes bielle-manivelle du compresseur. L’explication de la détérioration
rapide des dentures devient simple. Lors des marches à vide, quand le
couple moyen transmis est faible, les couples dynamiques sur les
roues dentées du réducteur entraînent l’inversion avec choc du contact
entre dentures.
Pour éliminer ce phénomène qui est à l’origine de la panne, on a
modifié la rigidité torsionnelle de l’accouplement élastique. Nous avons
retenu un accouplement de rigidité
K
3 = 23,78 x 108 N · m/rad (l’ancien
accouplement avait une rigidité K
3 = 3,6 x 106 N · m/rad). Les pulsa-
tions propres de cette nouvelle ligne d’arbres sont données dans le
tableau 6. La première pulsation propre n’est plus dangereuse pour le
fonctionnement de l’installation et expérimentalement nous avons
constaté la bonne tenue de la denture.
Tableau 6 – Pulsations propres du modèle du groupe
compresseur (figure 4) après modification de la rigidité
de l’accouplement
Mode norad/s tr/min
1 197,2 1 883
2 951,3 9 084
3 1 176 11 236
4 3 168 30 268