Evaluation

Prénom
Nom
Date
1
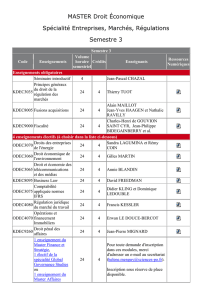
Capacités
Résoudre à l’aide d’un outil numérique des équations de la forme
f(x) = g(x)
Résoudre a l’aide d’un outil numérique des inéquations de la
forme f(x) ≥g(x)
Connaissances
Résolution graphique d’inéquations de la forme f(x) ≥g(x).
Compétences
Questions
Appréciationduniveau
d’acquisition
S’approprier
1
Analyser, Raisonner
4;5
Réaliser
2 ; 3
Communiquer
6
/10
Situation
Problématique : Maeva et Erwan veulent savoir qui aura le salaire le plus
élevé dans les années à venir
Evaluation sur la résolution d'équation et d'inéquation
Situation:
Le responsable d’une petite entreprise propose à ses deux employés Maeva et Erwan
une augmentation de salaire net suivant deux modes de calcul.
• Option A : une augmentation de 3 % au 1er janvier de chaque année
correspondant au tableau suivant.
Nombre d’années
depuis
le 1er janvier 2020
0
2
6
10
12
16
Salaire en centaine
d’euros
11,50
12,20
13,73
15,45
16,39
18,45
• Option B : une augmentation fixe de 43 € chaque 1er janvier.
Au 1er janvier 2020, le salaire net de Maeva et d’Erwan est de 1 150 €. Maeva
choisit l’option A et Erwan choisit l’option B.

Prénom
Nom
Date
2
1.Le salaire d’Erwan est modélisé par la fonction f. Montrer que
l’expression de f peut s’écrire f(x) = 11,5 + 0,43 x avec f(x) en centaines
d’euros et x en années.
2.Ouvrir le fichier « tab-salaires » pour afficher le tableau ci-contre.
a. Pour l’option A, sélectionner les valeurs du tableau et créer une liste
de points.
b. Pour l’option B, tracer la droite d’équation y = 11,5 + 0,43x.
3.Déterminer graphiquement, en utilisant l’icone les coordonnées
des points d’intersection des représentations des deux options.
4. En déduire l’année ou le salaire de Maeva sera égal à celui d’Erwan.
.......................................................................................
.......................................................................................
5. En déduire les années ou Erwan a un salaire supérieur à celui de Maeva.
.......................................................................................................................................................
.......................................................................................................................................................
6. Quelle est la formule la plus intéressante à long terme ?
.......................................................................................................................................................
.......................................................................................................................................................
Intersection
..................................................................................................................................................
..................................................................................................................................................
..................................................................................................................................................
..................................................................................................................................................
..................................................................................................................................................
..................................................................................................................................................
..................................................................................................................................................
..................................................................................................................................................