Loi uniforme continue — Wikipédia

Loi uniforme
continue

Uniforme
Densité de probabilité
Fonction de répartition
Paramètres
Support
Densité de probabilité
Fonction de répartition
Espérance
Médiane
Mode toute valeur dans
Variance

modifier (https://fr.wikipedia.org/w/index.php?title=Loi_uniforme_continue&action=edit&section=0)
Asymétrie
Kurtosis normalisé
Entropie
Fonction génératrice des moments
Fonction caractéristique
En théorie des probabilités et en statistiques, les lois uniformes continues forment une famille de lois
de probabilité à densité caractérisées par la propriété suivante: tous les intervalles de même
longueur inclus dans le support de la loi ont la même probabilité. Cela se traduit par le fait que la
densité de probabilités de ces lois est constante sur leur support.
La loi uniforme continue est une généralisation de la fonction rectangle à cause de la forme de sa
fonction densité de probabilité. Elle est paramétrée par les plus petites et plus grandes valeurs a et b
que la variable aléatoire uniforme peut prendre. Cette loi continue est souvent notée U(a, b).
Densité
La densité de probabilité de la loi uniforme continue est une fonction porte sur l'intervalle [a, b]:
Fonction de répartition
La fonction de répartition est donnée par
Fonctions génératrices
Fonction génératrice des moments
Caractérisation

La fonction génératrice des moments est
qui permet de calculer tous les moments non centrés, mk:
Ainsi, pour une variable aléatoire suivant cette loi, l'espérance est alors m1 = (a+b)/2 et la variance
est m2−m12 = (b−a)2/12.
Fonction génératrice des cumulants
Pour n≥2, le n-ième cumulant de la loi uniforme sur l'intervalle [0,1] est bn/n, où bn est le n-ième
nombre de Bernoulli.
Statistiques d'ordre
Soit X1, ..., Xn un échantillon i.i.d. issu de la loi U(0, 1). Soit X(k) la k-ième statistique d'ordre de
l'échantillon. Alors, la distribution de X(k) est une loi bêta de paramètres k et n−k+1. L'espérance est
Ce fait est utile lorsqu'on construit une droite de Henry.
Les variances sont
L'aspect uniforme
Propriétés

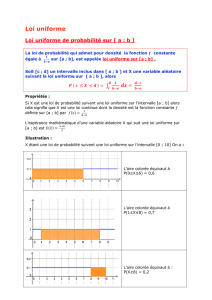
La probabilité qu'une variable uniforme tombe dans un intervalle donné est indépendante de la
position de cet intervalle, mais dépend seulement de sa longueur, à condition que cet intervalle soit
inclus dans le support de la loi. Ainsi, si X ≈ U(a, b) et que [x, x+d] est un sous-intervalle de [a,b], avec d
> 0 fixé, alors
qui est indépendant de x. Ce fait motive la dénomination de cette loi.
Le cas particulier a = 0 et b = 1 donne naissance à la loi uniforme standard, aussi notée U(0, 1). Il faut
noter le fait suivant: si u1 est distribué selon une loi uniforme standard, alors c'est aussi le cas pour
u2 = 1 – u1.
À toute partie A de borélienne, dont la mesure de Lebesgue λ(A) est finie et strictement positive,
on associe une loi de probabilité, appelée loi uniforme sur A, de densité de probabilité ƒ définie, pour
par:
où χA est la fonction indicatrice de l'ensemble A. La densité ƒ est donc nulle à l'extérieur de A mais
égale à la constante 1⁄λ(A) sur A.
Le cas particulier traité principalement dans cette page est le cas où d = 1 et où A est un intervalle [a,
b] de
Transport et invariance
Condition suffisante — La loi de la variable aléatoire Y =T(X), image, par une
transformation T, d'une variable X uniforme sur une partie A de est encore la loi
uniforme sur T(A) si T est, à un ensemble négligeable près, injectif et différentiable, et
si, presque partout sur A, la valeur absolue du jacobien de T est constante.
Loi uniforme standard
Loi uniforme sur l'ensemble A