Enoncés È Cours È
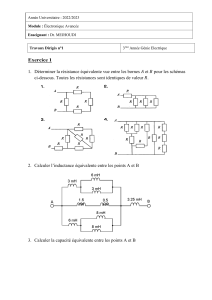
Exercice 1.1
I = E/(R + RC).
Avec RC = 10 Ω, I ≈ 1,2 A ; avec RC = 0 Ω, I ≈ 1200 A ! !
Si le fil ne fond pas, l’accumulateur va exploser (Puissance de l’ordre de 14 kW).
Exercice 1.2
Le générateur débite dans une résistance équivalente ρ = R.RC/(R + RC).
La tension aux bornes de A est : V = ρ.I = RC.IC ( = R.I0).
IC = ρ.I/RC = R.I/(R + RC).
Avec RC = 10 Ω, IC ≈ 5 mA ; avec RC = 10 kΩ, IC ≈ 4,81 mA
Avec R
C = 1 MΩ, I
C ≈ 1 mA : la source ne se comporte comme un générateur de courant que
si R est très supérieur à RC.
Exercice 1.3
La résistance équivalente à R2 // RC est : ρ = R.RC/(R + RC).
La tension aux bornes de R
C est V = E.ρ/(R1 + ρ) donc le courant qui circule dans R
C est :
I
V
R
E
R
R R R R R
CC C
= = + +
.
.( )
2
1 2 1 2
RC = 0 Ω, IC ≈ 6 mA V = 0 ; RC = 500 Ω, IC ≈ 3,42 mA V = 1,71 V
RC = 1 kΩ, IC ≈ 2,4 mA V = 2,4 V ; RC = 2 kΩ, IC ≈ 1,5 mA V = 3 V
RC = 100 kΩ, IC ≈ 0 mA V = 4 V
Le diviseur de tension n’est idéal que si RC >> R2
Exercice 1.4
I = K.Vn. I’/I = 300/100 = 3.
(45/33)n = 3 : ln3 = n.ln1,3636
n = 3,542.
0,1 A = K.333,542
K = 4,183.10–7 (système MKSA).
Équation de la droite de charge :
V2 = E – R.I = 40 – 100.I
Graphiquement, on tire :
I ≈ 85 mA ; V2 ≈ 31,5 V.
45 V
200 mA
Exercice 1.5
Équation de la droite de charge :
U = E – R1.I = 20 – 2000.I
On trace la caractéristique du dipôle équivalent à la lampe
et à R
2. (Additivité des courants pour une même tension).
L’intersection de cette nouvelle caractéristique avec la
droite de charge donne le point de fonctionnement. U = 5
V et I = 7,5 mA. Le courant dans la lampe est alors 5 mA.
Enoncés È Retour au menu È
5
5
10
10
I(mA)
U (V)
RI
1
/
1
100%