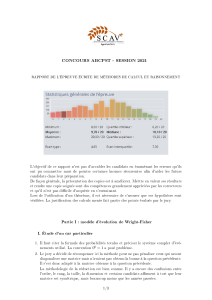
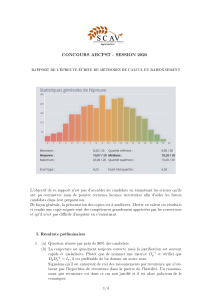
Rapport Concours ABCPST 2021 : Méthodes Calcul et Raisonnement

00= 1

P
P−1
Mnn= 1
Mn
Xn∈ {0,2N}Xn∈J0,2NK
u w

V(N1)V(N2)
λ W X 6= 0
N1+N2=N−N3N1+N2
1 2
•t7→ 1
√2πt
−t
21]0,+∞[(t)
Z2t7→ 1
√2πt
−t
21]0,+∞[(t)
•x
PZ2≤x=P(Z≤√x)
PZ2≤x=P(−√x≤Z≤√x)x
•
F
F
•
R+∞
0t fZ2(t)t
Z2
C