Conversion entre bases

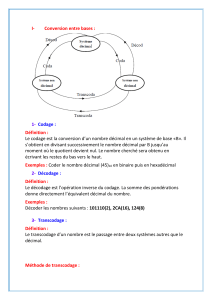
I- Conversion entre bases :
1- Codage :
Définition :
Le codage est la conversion d’un nombre décimal en un système de base «B». Il
s’obtient en divisant successivement le nombre décimal par B jusqu’au
moment où le quotient devient nul. Le nombre cherché sera obtenu en
écrivant les restes du bas vers le haut.
Exemples : Coder le nombre décimal (45)10 en binaire puis en hexadécimal
2- Décodage :
Définition :
Le décodage est l’opération inverse du codage. La somme des pondérations
donne directement l’équivalent décimal du nombre.
Exemples :
Décoder les nombres suivants : 101110(2), 2CA(16), 124(8)
3- Transcodage :
Définition :
Le transcodage d’un nombre est le passage entre deux systèmes autres que le
décimal.
Méthode de transcodage :

D’une manière générale pour transcoder un nombre d’une base «B1» en une
base «B2 », il faut décoder le nombre écrit en base «B1», puis coder le nombre
résultat du décodage, dans le système de base «B2».
Le transcodage peut être réalisé directement de la base «B1» vers la base «B2»
dans les cas particuliers suivants :
 Conversion hexadécimal – binaire :
Il s’agit de remplacer chacun symbole hexadécimal par les 4 bits appropriés,
comme l’illustre l’exemple suivant.
Déterminez l’équivalent binaire du nombre hexadécimal CF03(16)
 Conversion binaire – hexadécimal :
Il s’agit de diviser le nombre binaire en groupe de 4 bits et de remplacer chacun
de ces groupes par le symbole hexadécimal équivalent, comme l’illustre
l’exemple suivant.
Convertir 10101001101(2) en base 16
 Conversion Octal – binaire :
La base 8 est une puissance de la base 2. Pour convertir un nombre octal en
binaire, cela veut dire que pour représenter un seul chiffre octal en binaire, il
faut utiliser 3 bits.
Ainsi, la représentation des chiffres de la base 8 en binaire est la suivante :
Chiffre octal
Chiffre binaire équivalent
0
000
1
001
2
010
3
011
4
100
5
101
6
110
7
111
 Application 1 :
Soit le nombre octal X= (175)8 = ( ?) 2 :

Pour trouver l’équivalent binaire de ce nombre octal, il suffit de trouver
l’équivalent de chaque chiffre octal.
1
7
5
0
0
1
1
1
1
1
0
1
X= (175)8= (1111101)2
 Application 2 :
Soit le nombre binaire Y= (1111101)2 = ( ?) 8 :
Pour trouver l’équivalent octal de ce nombre binaire, il faut :
- Regrouper les bits du nombre binaire en groupe de 3bits en partant de la
droite. Si le dernier groupe ne contient pas trois bits, ajouter des zéros.
- Trouver l’équivalent octal de chaque groupe de 3 bits
0
0
1
1
1
1
1
0
1
1
7
5
Y= (1111101)2 = (175) 8 (les deux zéros sur la gauche sont superflus)
Y1 = (11001010010110)2 = (011 001 010 010 110)2 = (31226)8
Y2 = (110010100,10101)2 = (110 010 100,101 010)8 = (624,51)8
 Conversion hexadécimal – Octale :
Pour convertir de l’hexadécimal à l’octal le plus simple est de passer par le
binaire
Exemple :
(1, BSC) 16 = ( ?)8
Etape 1 : on regroupe par 4 bits
Etape 2 : on regroupe par 3 bits
Octal
Binaire
Binaire
Octal

Résultat : (15,534)8
II- Opérations arithmétiques en binaire :
Addition binaire : L'addition de deux nombres binaires est parfaitement
analogue à l'addition de deux nombres décimaux.
0 + 0 = 0
1 + 0 = 1
1 + 1 = 10
1 + 1 + 1 = 11
Soustraction binaire : la soustraction en binaire est également basée sur la
notion de retenue. Cependant, dans le système binaire, il n'y a que deux
chiffres dont le plus grand est 1.
0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
0 - 1 = 1
Multiplication : La multiplication binaire s’effectue selon le principe des
multiplications décimal, on multiplie donc le multiplicande par chacun des bits
du multiplicateur.

Division : la multiplication était basée sur une succession d’addition
inversement la division va être basée sur une succession de soustraction.
III- La complémentation :
1- Représentation des entiers signés :
Ce sont des nombres possédant un signe + ou -, il existe 3 méthodes pour les
représenter :
a) SVA : Signe et Valeur Absolue
b) Cà1 : Complément à 1
c) Cà2 : Complément à 2
1-1- Signe et Valeur Absolue (SVA) :
Si un nombre est représenté sur n Bits, alors la valeur absolue du nombre est
codée sur (n-1) bits
 0 : représente un nombre positif
 1 : représente un nombre négatif
Exemple :