Circuits Magnétiques: Exercices Corrigés

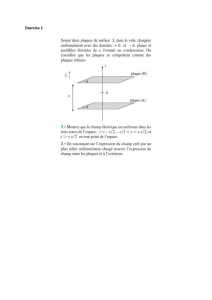
Exercices sur les circuits magnétiques : corrigé
Exercice I
Un circuit magnétique est constitué d'un tore en matériau ferromagnétique
de perméabilité relative 1000, de longueur moyenne 200 mm, de section
10 cm² et d'un entrefer de 1 mm de long.
Sur ce circuit, on enroule 25 spires d’un conducteur parcouru par un
courant de 2 A.
On suppose que le champ dans le fer est 1,25 fois plus important que dans
l'entrefer.
Calculer en utilisant le théorème d'Ampère le module du champ magnétique dans l'entrefer et les excitations
magnétiques dans l'acier et l'entrefer.
Exercice II
Une bobine est constituée de 30 spires enroulées sur un circuit magnétique constitué d'un matériau
ferromagnétique de perméabilité relative µr = 1000 et d'un entrefer de 1 mm, la fibre moyenne mesure
300 mm. La section du fer est de 10 cm² et celle supposée de l'entrefer de 12 cm².
1. L’intensité du courant dans le bobinage étant de 8 A, calculer le champ magnétique dans l'entrefer.
Le circuit magnétique est décomposé en une partie « acier » et en une partie « air » :
•Partie « acier » : longueur
la=300.10−3 m
, section
Sa=10.10−4 m2
et perméabilité magnétique
a=4.10−4 SI
•Partie « air » : longueur
le=10−3 m
, section
Se=12.10−4 m2
et perméabilité magnétique
a=4.10−7 SI
D'après le théorème d'Ampère :
Ha.laHe.le=N I
avec Ha et He les modules de l'excitation dans l'acier
et l'entrefer, N = 30 spires et I l'intensité du courant dans le bobinage.
Comme
Ba=aHa
et
Be=0He
, l'équation précédente devient
Ba
a
.laBe
0
.le=N I
D'après la loi de conservation du flux :
Ba.Sa=Be.Se
avec Ba et Be les modules du champ magnétique
dans l'acier et l'entrefer. On obtient
Ba=Be.
Se
Sa
D'où
Be
Se
Sa
1
a
.laBe
0
.le=N I
qui devient
BeSe
Sa
1
a
.la1
0
.le=N I
en factorisant Be et
finalement
Be=N I
Se
Sa
1
a
.la1
0
.le
=30. 8
12.10−4
10.10−4
1
4.10−4. 300.10−31 4.10−7. 10−3
=0,221 T
2. Quelle est le flux à travers le circuit magnétique ?
Puisque
=Ba.Sa=Be.Se
alors
=Be.Se=0,221 . 12.10−4=265 µWb
3. Calculer le flux total vu par la bobine.
C'est le flux vu par une spire (flux à travers une section du circuit magnétique) multiplié par le nombre de
spires :
T=N=30 .265=7,95 mWb
Exercices sur les circuits magnétiques :
CorrigéPage 1/6 TS1 ET 2011-2012

Exercice III
On considère un circuit magnétique torique de section carrée
sur lequel est bobiné un enroulement de N = 20 spires
parcourues par un courant d’intensité I.
La perméabilité relative de l'acier vaut 10000.
Rayon intérieur R1 = 4 cm.
Rayon extérieur R2 = 6 cm.
Épaisseur de l'acier 2 cm.
La longueur de l'entrefer est variable
I
R
2
R
1
e
La section de l'entrefer est supposée égale
à celle de l'acier.
1. En utilisant la relation d’Hopkinson, écrire le flux à travers une section du matériau en fonction de
l'épaisseur e de l'entrefer et du courant I (la longueur de l'entrefer est négligée pour le calcul de la réluctance
de l’acier).
2. Calculer l'intensité du courant permettant d'obtenir un champ magnétique de 100 mT.
a. lorsque l'entrefer est nul.
b. lorsque l'entrefer vaut 0,5 mm.
3. L'énergie W emmagasinée par la bobine s'écrit :
W=1
2T.I
, ΦT étant le flux total vu par la bobine.
a. Exprimer l'énergie en fonction de e et Φ.
b. Tracer la courbe W = f(e) (énergie stockée en fonction de la longueur d'entrefer) pour la même valeur
du flux qu'au 2 (e varie de 0 à 3mm). Dans quelle partie du circuit magnétique l'énergie est-elle
majoritairement stockée ?
Exercices sur les circuits magnétiques :
CorrigéPage 2/6 TS1 ET 2011-2012

Exercice IV
On réalise une bobine de 20 spires sur le noyau
central du circuit magnétique ci-contre :
La perméabilité relative du matériau vaut 1000.
1. Le circuit magnétique peut être représenté par le
schéma ci-dessous à droite (analogie électrique) :
a. Calculer les valeurs des réluctances de chaque
partie du circuit magnétique (On suppose que les
sections des entrefers sont égales à celles des pôles
qui les encadrent. On néglige la longueur de
l'entrefer pour le calcul des réluctances des parties
fer).
2 cm 2 cm
5 cm
0,5 cm0,5 cm
10cm
2 cm
7 cm
7 cm
entrefer
0,1 cm
La réluctance d'une portion de circuit magnétique est donnée par
ℜ= 1
l
S
Les longueurs sont celle de la fibre moyenne du circuit, les notation sont celles du circuit magnétique
analogue de le figure suivante :
Pour les colonnes verticales latérales :
ℜ1=1
a
l1
S1
avec l1 = (7 – 1) = 6 cm, S1 = 2x7 = 14 cm2 et la
perméabilité magnétique
a=0.r
avec
r=1000
. Ce qui donne :
ℜ1=1
4. 10−7. 1000
6.10−2
14.10−4=34,1 kH−1
Pour les portions verticales et latérales de la colonne horizontale inférieure :
ℜ2=1
a
l2
S2
avec l2 = 1 cm,
S2 = 2x7 = 14 cm2 et la perméabilité magnétique
a=0.r
. Ce qui donne :
ℜ2=1
4. 10−7. 1000
10−2
14.10−4=5,7 kH−1
Pour les portions horizontales de la colonne horizontale supérieure :
ℜ3=1
a
l3
S3
avec l3 = (5 – 1) =
4 cm, S3 = 2x7 = 14 cm2 et la perméabilité magnétique
a=0.r
. Ce qui donne :
ℜ3=1
4. 10−7. 1000
4.10−2
14.10−4=22,7 kH−1
Pour la colonne centrale :
ℜ4=1
a
l4
S4
avec l4 = (7 – 1) = 6 cm, S4 = 5x7 = 35 cm2 et la perméabilité
magnétique
a=0.r
. Ce qui donne :
ℜ4=1
4.10−7. 1000
6.10−2
35.10−4=13,6 kH−1
Pour la portion verticale et centrale de la colonne horizontale inférieure :
ℜ5=1
a
l5
S5
avec l5 = 1 cm,
S5 = 5x7 = 35 cm2 et la perméabilité magnétique
a=0.r
. Ce qui donne :
ℜ5=1
4. 10−7. 1000
10−2
35.10−4=2,8 kH−1
Pour les entrefers extérieurs :
ℜe1 =1
0
le1
Se1
avec le1 = 0,1 cm, Se1 = 2x7 = 14 cm2 et la perméabilité
magnétique du vide (ou de l'air). Ce qui donne :
ℜe1=1
4. 10−70,1 .10−2 14.10−4=568 kH−1
Exercices sur les circuits magnétiques :
CorrigéPage 3/6 TS1 ET 2011-2012

Pour l'entrefer central :
ℜe2 =1
0
le2
Se2
avec le2 = 0,1 cm, Se2 = 5x7 = 35 cm2 et la perméabilité magnétique
du vide (ou de l'air). Ce qui donne :
ℜe2=1
4. 10−70,1 .10−2 35.10−4=227 kH−1
b. Mettre le schéma sous la forme d’une force magnétomotrice
« alimentant » une réluctance, le flux dans le circuit étant celui
de la colonne centrale.
Les réluctances des branches extérieures sont en série (même flux),
la réluctance équivalente est égale à la somme des réluctances :
ℜlat=2. ℜ3ℜ1ℜ2ℜe1
ℜlat=2. 22,734,15,7568=653 kH−1
Ces deux réluctances sont en parallèle et comme elle sont
identiques, elle peuvent être remplacées par une seule égale à
ℜlat
2=653 2=326 kH−1
Les réluctances de la branche centrale sont en série soit
ℜcent=ℜ4ℜ5ℜe2=13,62,8227=243 kH−1
Finalement, les réluctances
ℜlat
2
et
ℜcent
sont en série ce qui donne une réluctance équivalente :
ℜeq=ℜlat
2ℜcent =326243=569 kH−1
2. Module du champ magnétique
a. Calculer la valeur du courant permettant d'obtenir un champ de 140 mT dans l'entrefer central.
D'après la relation d'Hopkinson
ℜeq =N I
avec F le flux dans le circuit magnétique, N le nombre de
spires et I l'intensité du courant dans la bobine.
La section Sc de l'entrefer central est égale à 35 cm2 et les vecteurs champ magnétique
Bc
et surface sont
supposés colinéaires et de même sens donc
=  Bc. Sc=Bc.Sc
et la relation d'Hopkinson devient
ℜeq Bc.Sc=N I
ce qui donne :
I=ℜeq Bc.Sc
N=569.103.0,14 .35.10−4 20 =13,9 A
b. En déduire le champ magnétique dans les colonnes extérieures.
D'après la loi de conservation du flux :
Bext .Sext =Bc.Sc
(indice « ext » pour extérieur) soit
Bext=Bc.
Sc
Sext
=0,14 . 35
14 =0,35 T
3. Calculer le flux dans la bobine et le rapport de ce flux sur l'intensité du courant dans la bobine.
La bobine est constituée de 20 spires qui « voient » chacune
=Bc.Sc
soit un flux total :
T=20. =20. Bc.Sc=20 . 0,14 . 35.10−4=9,8 .10−3 Wb
Le rapport du flux sur l'intensité du courant :
T
I=9,8 .10−3 13,9 =7,05 .10−4 H
(c'est l'inductance de la
Exercices sur les circuits magnétiques :
CorrigéPage 4/6 TS1 ET 2011-2012

bobine).
Exercice V
On considère l'électroaimant ci-contre. Les cotes sont données en mm, la
profondeur est égale à 30 mm. Perméabilité relative des culasses et du
noyau : 1500.
Le ressort de rappel maintient la partie mobile dans une position telle que
l'on ait un entrefer de 2,5 mm sur chaque branche.
1. Exprimer l'énergie W emmagasinée par la bobine en fonction du flux F
à travers une section du circuit magnétique, du nombre de spires et du
courant I qui la traverse.
Relation de l'exercice III question 3 :
W=1
2T.I
et
T=N
avec N le
nombre de spires. Finalement
W=1
2N.I
2. Exprimer le flux F en fonction de la réluctance du circuit magnétique,
du nombre de spires et du courant I. En déduire l'expression de W en
fonction de la réluctance du circuit, du nombre de spires et du courant I.
10
10
10 10
20
40
40
D'après la relation d'Hopkinson
ℜ=N I
avec
ℜ
la réluctance du circuit magnétique, F le flux dans le
circuit magnétique, N le nombre de spires et I l'intensité du courant dans la bobine.
3. Donner la réluctance en fonction de la longueur x d'un entrefer.
La longueur de la fibre moyenne de l'acier est
la=2 .302. 35=130 mm
et sa section
Sa=10 . 30=300 mm2
soit une réluctance
ℜa=1
0.a
la
Sa
=1
4.10−7.1500
130.10−3
300.10−6=230 kH−1
La réluctance de l'entrefer dépend de sa longueur :
ℜe=1
0
x
Se
=1
4. 10−7
x
300.10−6=2,65 .109.x(en H−1 et x en m)
La réluctance du circuit est égale à la somme de ces deux réluctances soit :
ℜe=230.1032,65 .109.x(en H−1 et x en m)
4. Exprimer l'intensité F de la force de rappel en fonction de x (
F=dW
dx
)
On remplace W par son expression dans
F=dW
dx
ce qui donne
F=d
dx 1 2N.I
et comme
= N I
ℜ
alors
F=d
dx 1 2NN I
ℜ.I=1
2N.I2d dx 1
ℜ
(le produit
1
2N I 2
est constant)
En remplaçant
ℜ
par son expression :
F=1
2N.I2d dx 1
230.1032,65.109.x
Dérivée de
230.1032,65.109.x
:
d
dx 1
230.1032,65.109.x= −2,65.109.x 230.1032,65 .109.x2
D'où l'expression de la composante verticale de la force :
Fv=− 1
2N.I22,65.109
230.1032,65.109.x2
soit une
Exercices sur les circuits magnétiques :
CorrigéPage 5/6 TS1 ET 2011-2012