chapitre3-Transfert-Thermique

Notes de Cours de Transfert Thermique Ayadi Mahfoudh &Houda Oukabi
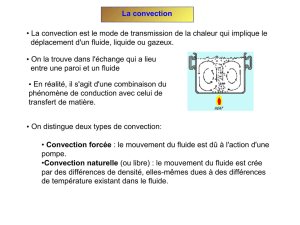
1
Université de Carthage Ecole Nationale d’Ingénieurs de Bizerte AU : 20/21
Chapitre III
TRANSFERT THERMIQUE
PAR CONVECTION
1. Généralités et notions de base
Dans tous les problèmes que nous avons traités jusqu'à présent, nous avons supposé que le
coefficient d'échange thermique intervenant dans la loi de Newton était connu a priori. Or,
dans la plupart des applications de la thermique, la détermination du coefficient d'échange est
précisément la partie la plus délicate. En effet, dans les transferts de chaleur par convection,
la conduction thermique déjà présente dans les solides s'ajoute l'advection, transfert d'énergie
induit par l'écoulement, ce qui introduit un niveau de complexité supplémentaire. De façon
générale, le but de ce chapitre est donc la détermination du coefficient d'échange thermique.
On notera h le coefficient d’échange local en un point de la surface d’échange. Notons que h
n'est pas nécessairement uniforme, il est susceptible de varier dans l'espace.
1.1Convection
Le transfert de chaleur par convection est associé à un déplacement de matière (fluide), les
particules chaudes en mouvement peuvent migrées vers des zones moins chaudes. Ainsi le
type d'écoulement est important dans la description du problème.
Lorsque le mouvement du fluide se produit naturellement sous l’effet de la variation de la
densité et des forces de gravité, la convection serait qualifiée de libre ou naturelle. Si le
mouvement du fluide est provoqué par une cause extérieure (ventilateur, pompe…) la
convection serait dite forcée
1.2 Régime d’écoulement
Les particules fluide en mouvement peuvent décrire des trajectoires régulières, autrement les
lignes de courant restent parallèles, l’écoulement est dit laminaire. L’écoulement est dit
turbulent lorsqu’il n’y pas de direction privilégiée. Les particules fluides se déplacent dans
toutes les directions.
1.3 Problème de la convection
Chaque situation fait intervenir de nombreux paramètres descriptifs. Le problème majeur pour
calculer le flux de chaleur transféré par convection est la détermination du coefficient
d’échange h. Considérons l’exemple d’un fluide en circulation forcée dans une canalisation
(figure3.1) pour lequel on se propose de déterminer le coefficient de convection h
caractérisant le transfert de chaleur fluide-paroi.
Figure 3.1 : Paramètres de convection pour un écoulement forcé
V

Notes de Cours de Transfert Thermique Ayadi Mahfoudh &Houda Oukabi
2
Université de Carthage Ecole Nationale d’Ingénieurs de Bizerte AU : 20/21
Les paramètres descriptifs du transfert par convection forcée de cette application sont illustrés
dans le tableau 3.1. Huit grandeurs peuvent intervenir dans le calcul du flux avec 4
dimensions fondamentales représentant respectivement la longueur L, la masse M, le temps T
et la température θ.
Remarques
1. Lorsque les grandeurs mécaniques et grandeurs thermiques ne permettent pas sera la
mesure de l'échange d'énergie, on ajoutera la quantité de chaleur Q qui sera considérée
comme une 5ième dimension.
2. Q est homogène à un travail qui s'exprime en fonction des dimensions fondamentales
M, L et T par Q = M.L. T -2 n'est pas une vraie dimension fondamentale.
Tableau 3.1: Paramètres descriptifs
Grandeur
symbole
Unité SI
Equations aux
dimensions
Diamètre du tube
D
m
L
Vitesse du fluide
V
m.s-1
LT-1
Masse volumique du fluide
ρ
Kg.m-3
ML-3
Viscosité dynamique du fluide
η
Kg.m-1s-1
ML-1T-1
Conductivité thermique du fluide
λ
W.m-1.K-1
MLT-3θ-1
Chaleur massique du fluide
Cp
J.Kg-1K-1
L2T-2θ-1
Coefficient d’échange convectif
h
W.m-2K-1
MT-3θ-1
Ecart de température
Tf-Tp
K
θ
Densité de flux
φ
W
ML2T-3
2. Analyse dimensionnelle
2.1 Principe de la méthode
Le tableau 4.1 montre qu’on peut exprimer les grandeurs physiques en fonction d'un nombre
limité de dimensions fondamentales. La méthode d’analyse dimensionnelle repose sur le
principe de l’homogénéité des termes d’une équation connue sous le nom de théorème de
Vaschy-Buckingam ou théorème des groupements π.
Une loi physique exprime une variable physique G1 en fonction d'un certain nombre d'autres
variables physiques indépendantes G2, G3,….., Gn cela pourra se traduire par une relation du
type :G1=f(G2,G3,…,Gn). Cela montre que la loi physique peut être présentée par une relation
de la forme : F(G1,G2,…,Gn)=0.
Le nombre de variables intervenants dans cette relation est souvent élevé, ce qui est le cas
pour un problème de transfert par convection, une simplification du problème serait exigée
celle-ci pourra s’effectuer de la manière suivante :
 On écrit pour chaque variable Gi, l'équation aux dimensions en fonction des
dimensions fondamentales. On dispose alors de n équations qui ont nécessité p
dimensions fondamentales pour caractériser toutes les grandeurs physiques.
 On prélève p de ces n variables que l'on considère comme variables de base (chaque
variable est définie par une équation de base). Cela permet d’obtenir ce qu’on appelle
équations de base. Bien que le choix des équations prélevées soit arbitraire, il faut
toutefois que chaque dimension fondamentale apparaisse au moins une fois sur
l'ensemble des p équations.

Notes de Cours de Transfert Thermique Ayadi Mahfoudh &Houda Oukabi
3
Université de Carthage Ecole Nationale d’Ingénieurs de Bizerte AU : 20/21
 Les (n-p) variables restantes seront présentées alors sous forme de (n-p) rapports sans
dimensions appelés groupements qui sont des "grandeurs réduites". Cela permet de
transformer la loi physique pour qu’elle soit présentée sous la forme d’une relation du
type:
0
2121321 21  ),...,,(.....),....,,( pn
n
p
nn
ngDDDGGGGF q
Le terme g(π1,π2,…,πn-p) qui devra être nulle constitue ce qu’on appelle une équation
réduite de la loi physique: g(π1,π2,…,πn-p)=0
les relations définissant D1, ….., Dp formes les équations de base
Un groupement
i est défini par une équation sans dimension. Il est obtenu par le rapport entre
une grandeur physique n'appartenant pas à l’ensemble des équations de base et le produit des
équations de base, chacune d'elle étant portée à une puissance qu’on devra déterminer:
p
a
p
aa i
iGGG
G
...... 21 21
avec (i=p+1,p+2,…, p+(n-p))
Pour chaque dimension fondamentale M, L, T et θ figurant au dénominateur, on fait la somme
des exposants que l'on identifie avec l'exposant de la même dimension figurant dans l'équation
dimension de la grandeur physique du numérateur. On obtient ainsi un système linéaire de p
équations dont la résolution permet de déterminer les p exposants des équations de base du
dénominateur.
Il suffit alors d'écrire le rapport en fonction des grandeurs physiques attachées aux équations
dimensions de départ.
Théorème de Vaschy-Buckingam
Toute fonction F de n variables indépendantes Gi mesurées par p unités
fondamentales (avec n>p) s’exprime nécessairement sous la forme:
0
2121321 21  ),...,,(.....),....,,( pn
n
p
nn
ngDDDGGGGF q
les variables D1, D2, …,Dp étant choisies dimensionnellement indépendantes. Les
fonctions πi sont des groupements adimensionnels des variables D1, D2, …,Dp.
2.2 Détermination des groupements adimensionnels
2.2.1 Démarche d’analyse
On se propose de traiter les échanges par convection entre un fluide en circulation forcée dans
une canalisation cylindrique pour lequel on se propose de déterminer le coefficient de
convection h relatif au transfert de chaleur fluide-paroi qui correspond à une convection
forcée.
Il faut déterminer en premier lieu tous les paramètres dont dépend la densité de flux de
chaleur φ qui est liée à h par la relation φ= h(Tp-Tf).
Ces paramètres sont respectivement
 les caractéristiques du fluide (tableau 3.2),
 la vitesse d’écoulement V,
 le diamètre de la conduite D
 la différence de température (Tp-Tf)

Notes de Cours de Transfert Thermique Ayadi Mahfoudh &Houda Oukabi
4
Université de Carthage Ecole Nationale d’Ingénieurs de Bizerte AU : 20/21
Tableau 3.2 : Caractéristiques du fluide
Grandeur
symbole
Equation aux
dimensions
Masse volumique du fluide
ρ
ML-3
Viscosité dynamique du fluide
η
ML-1T-1
Conductivité thermique du fluide
λ
MLT-3θ-1
Chaleur massique du fluide
cp
L2T-2θ-1
La loi recherchée serait représentée par une relation du type :
F(ρ ,η, λ, cp, V, D, h, Tp-Tf )=0
Il faut choisir ensuite 4 (p=4) variables de base de façon à ce que les 4 dimensions
fondamentales figurent au moins une fois dans l'ensemble des variables. Prenons par exemple
ρ , λ, η et D comme variables de base, il reste les variables V, cp, h et Tp-Tf
On écrit alors les 4 rapports sans dimension correspondants à ces variables sous la forme :
1111
1dcba D
V
,
2222
2dcba p
D
c
,
3333
3dcba D
h
et
4444
4dcba fp
D
TT
2.2.2 Calcul des exposants
Pour calculer les exposants des puissances on doit remplacer dans chaque rapport πi les
grandeurs physiques par leurs équations dimensions ce qui donne par exemple pour π1 :
1111111111
1
1111111 33
1
11133
1
1bcbdcbacba
d
cbadcba TLM LT
LTMLMLTML
LT
D
V
Pour chaque dimension fondamentale, on identifie les exposants de puissance entre
numérateur et dénominateur relatifs à une même dimension ce qui conduit au système :
a1+b1+c1=0
-3a1+b1-c1+d1=1
-3b1-c1=-1
-b1=0
La résolution des équations donne les valeurs des différents exposants soit:
a1=-1, b1=0, c1=1 et d1=-1
Cela donne :
e
dcba R
VD
D
V
D
V 
1101
11111
La même démarche d’identification serait appliquée aux trois groupements restants, en
remarquant que les 4 groupements ne diffèrent que par leurs numérateurs respectifs. Le
tableau 3.3 récapitule les résultats des calculs développés.

Notes de Cours de Transfert Thermique Ayadi Mahfoudh &Houda Oukabi
5
Université de Carthage Ecole Nationale d’Ingénieurs de Bizerte AU : 20/21
Tableau 3.3 : Identification des groupements adimensionnels
Groupement
Dimension
numérateur
Système
d’équations
Solutions
Nombre sans
dimension
Dénomination
du
groupement
1111
1dcba D
V
LT-1
a1+b1+c1=0
-3a1+b1-
c1+d1=1
-3b1-c1=-1
-b1=0
a1=-1
b1=0
c1=1
d1=-1
VD
Re
Nombre
de Reynolds
2222
2dcba p
D
C
L2T-2θ-1
a2+b2+c2=0
-3a2+b2-
c2+d2=2
-3b2-c2=-2
-b2=-1
a2=0
b2=1
c2=-1
d2=0
p
r
C
P
Nombre de
Prandtl
3333
3dcba D
h
MT-3θ-1
a3+b3+c3=1
-3a3+b3-
c3+d3=0
-3b3-c3=-3
-b3=-1
a3=0
b3=1
c3=0
d3=-1
hD
Nu
Nombre de
Nusselt
4444
4dcba fp
D
TT
θ
a4+b4+c4=0
-3a4+b4-
c4+d4=0
-3b4-c4=0
-b4=1
a4=-2
b4=-1
c4=3
d4=-2
3
22
)( fp
b
TTD
N
rc
e
bPER
N.
2
Le groupement
4
peut être exprimé en fonction de Pr et Re :
T
V
R
P
Ce
r
p 2
2
4
Cela conduit à identifier un autre nombre sans dimensions connu sous le nom de nombre
d’Eckert:
TCV
E
p
c
2
2.3 Intérêt de l’analyse dimensionnelle
La méthode de l’analyse dimensionnelle fournit les grandeurs réduites exploitables pour
déterminer les lois de transfert. Ces lois sont de la forme :
g(Nu, Re, Pr, Ec)=0
Les variables réduites sont exploitables pour la représentation, la comparaison et la recherche
des résultats expérimentaux :
- la représentation des résultats expérimentaux est simplifiée, on pourra avoir une
courbe reliant 2 variables ou un abaque reliant 3 variables au lieu d’une relation liant
(3+p) paramètres
- la comparaison des résultats expérimentaux est aussi rapide et aisée, quelque soit le
chercheur même si le système d’unité utilisé est différent puisque les grandeurs
réduites sont sans dimension.
- La recherche des résultats expérimentaux est facilitée et ordonnée: s’il suffit de tracer
une courbe entre deux variables réduites, c’est qu’il suffit d’effectuer une seule série
d’expériences.