Dipôle RC ( bac scientifiques svt pc sm )

Dipôle RC
1-Le condensateur.
Un condensateur est constitué de deux armatures A et B
conductrices séparées par un isolant.
Nous admettrons qu'à chaque instant, les
armatures A et B portent des charges
électriques opposées, de mêmes valeurs
absolues : qA = - qB .
A B
qA qB
+
+
+
+
-
-
-
-
1-1-Définition :
1-2-Charge électrique et intensité.
Symbole du
condensateur
Par définition , l’intensité i du courant est le débit de charge
transportées, c’est à dire à la charge électrique transportée
par unité de temps : Donc
A
dq
i(t)= dt
A B
qA qB
+
(A) (C) coulomb
(s)
Algébrisation de l’intensité du courant :
☞ i(t) > 0 ⇒
☞ i(t) < 0 ⇒
A
dq >0
dt
A
dq <0
dt
qA ↗
⇒
qA ↘
⇒
⇒
⇒
le condensateur se charge
décharge du condensateur

1-3-La relation entre la tension uAB et la charge qA On réalise le montage ci-contre . On
ferme l’interrupteur K. Et on mesure la
tension uAB au bornes du condensateur
en fonction du temps. On obtient Une
fonction linéaire , donc : générateur de courant
continu (I0 = cte)
UAB = k.t ❶
Et puisque I0=constante, donc
A
0
dq
I =i= dt
A0
q =I .t
❷
A
AB
q
U
0
I
=k
=C
(C) (F) (V)
❶
❷ d'où
A AB
q =C.U
C représente la capacité du condensateur , son unité dans
S.I est le farad (F) .
uAB la tension au bornes du condensateur en (V) .
qA la charge du condensateur en (C) .
Les sous multiples du farad:
-3
1mF =10 F
-6
1μF =10 F
-9
1nF =10 F
-12
1pF =10 F
2-Association des condensateur 2-1-Association en parallèle
K
A
V
I0
I0
UAB
B
.
A
.

i i
q1 C1
q2 C2
A B
.
.
A B
.
.
q Céq
UAB
UAB
Selon la loi des nœuds: q = q1+q2 Céq.UAB = C1.UAB + C2.UAB
Céq = C1 + C2
D'où
On peut généraliser ce résultat pour un nombre
n de condensateur branché en parallèle
n
i
éq i=1
C = C
Utilité de cette association :
Amplifier la capacité. On peut , sous une faible tension , obtenir
une très grande charge électrique que un condensateur seul ne
peut pas la fournir .
2-2-Association en série
i
A B
.
.
q Céq
UAB
UAB
A B
D
.
.
.
i q1 C1 q2 C2
La branche AB est traversée par la même intensité du
courant i, c’est à dire q1 = q2 = q
On applique la loi d’additivité des tensions entre A et B :

On peut généraliser ce résultat pour un
nombre n de condensateur branché en série :
n
i=1 i
éq
11
=
CC
Utilité de cette association :
On peut obtenir un capacité de faible valeur en appliquant une
haute tension que chaque condensateur ne peut pas la
supporter.
12
12
qq
q=+
C C C
12
1 1 1
=+
C C C
UAB = UAD + UDB
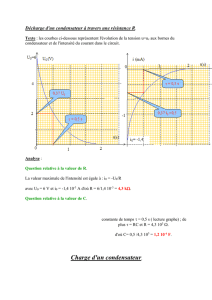
3-Réponse d’un dipôle RC à un échelon de tension:
3-1-Réponse à un échelon montant de tension (charge du condensateur)
Échelon de tension est un signal électrique u(t) . On distingue
deux types :
u(t)
t
E
0
t 0 ona: u(t)=
t > 0 ona: u(t E)=
0
Échelon montant de tension
E u(t)
t
0
t 0 ona: u(t)=
t > 0 ona: u(t 0)=
E
Échelon descendant de tension
< <

a-Équation différentielle vérifiée par la tension uC .
B
uR R
E
.
.
.
.
K
u uC A C
i > 0
y
On considère le montage électrique
suivant :
A l’instant t0 = 0, on ferme
l’interrupteur K. La tension aux
bornes du dipôle RC
passe de 0 à E
D’après l’additivité des tensions on peut écrire :
et d’après la loi d’Ohm on a:
CR
u=u +u =E
R
u =R.i
C
C
du
E=u +RC dt
dq
=R. dt
C
dC.u
=R. dt
C
du
=RC. dt
Équation différentielle
vérifiée par la tension uC
Remarque : Puisque
C
q
u=
C
dq
RC. +q= C.E
dt
Donc
b-Solution de l’équation différentielle :
On montre, que la solution de cette équation différentielle est :
uC(t) = Ae−mt +B , telle que A , B et m des constantes à
déterminer.
En portant cette solution dans l’équation différentielle,