CHARGE ET INTERACTIONS ELECTROSTATIQUES
I. Introduction
L'électrostatique est la branche de la physique qui étudie les phénomènes (champ et potentiel
électrostatique) créés par des charges électriques statiques pour l'observateur. Les forces
électrostatiques sont décrites par la loi de Coulomb qui présente une certaine analogie avec
l’interaction gravitationnelle.
II. Différents modes d’électrisation
Depuis l’antiquité (Thalès de Milet, 4ème siècle avant J. C), certaines substances frottées
comme l’ambre attirent les corps légers.
On admet, aujourd’hui, que le frottement fait apparaître des charges électriques, c’est le
phénomène de l’électrisation. On trouve plusieurs modes d’électrisation :
2-1. Electrisation par frottement
Certains corps frottés acquièrent la propriété d’attirer les corps légers. On dit qu’ils sont
électrisés par frottement.
Dans certains matériaux, l’électrisation peut se répartir en tous leurs points, ce sont les
conducteurs, dans d’autres, elle ne se manifeste que sur la partie frottée, ce sont les isolants.
Dans tous les cas, l’électrisation représente un phénomène de transfert de charges.
2-2. Electrisation par contact
On prend une baguette électrisée A et on la met en contact avec une autre baguette de verre non
électrisée B, nous constatons, après séparation, que cette dernière possède à son tour la propriété
d’attirer les corps légers. On dit qu’elle s’est électrisée par contact.
2-3. Electrisation par influence
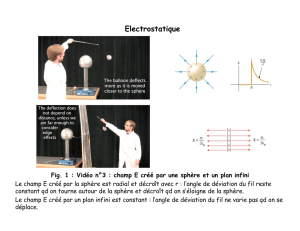
On utilise un pendule électrique, qui se compose par exemple, d’une petite boule de moêlle de
sureau suspendue par un fil de soie à un support (Fig. 1).

Figure 1
Quand on approche un corps électrisé, la boule est attirée, car elle s’est électrisée par influence.
Ce phénomène d’influence est à l’origine de l’attraction des petits morceaux de papier.
III. Les deux espèces d’électricité
On frotte une baguette de verre avec un morceau de drap et on met l’extrémité B (frottée) de la
baguette électrisée en contact avec la boule d’un pendule électrique. Dès que B s’approche de
la boule, il y a répulsion de la boule de sureau par B (Fig. 2).
Figure 2
Maintenant, si on remplace la baguette de verre par un bâton d’ébonite frotté avec une peau de
chat, il y a attraction (Fig. 3).
Figure 3

A partir de ces deux possibilités (attraction ou répulsion), on peut déduire l’existence de deux
espèces d’électricité. On les désigne sous le nom de charges positive (+) et charge négative (-
).
L’expérience montre qu’il y a attraction entre des charges de signes différentes et répulsion
entre des charges de mêmes signes.
La charge macroscopique positive d’un corps est due à un manque d’électrons de ce corps et la
charge négative est due à un excès d’électrons.
IV. La charge électrique
4-1. Définition
La charge électrique d’une particule est une grandeur scalaire (algébrique) qui caractérise les
actions électromagnétiques subies ou exercée par la particule.
La charge électrique joue dans l’interaction électrostatique le même rôle que joue la masse
(scalaire positive) dans l’interaction gravitationnelle.
4-2. Quantification de la charge
A l’échelle microscopique, l’expérience de Millikan (1913) montre que la charge électrique
varie de façon discontinue et se présente sous forme de quantité bien déterminée. On dit qu’elle
est quantifiée. Sa valeur est un multiple entier d’une charge qu’on peut prendre comme charge
élémentaire, notée e. Celle-là est bien la valeur absolue de la charge d’un électron e = 1,60219
10-19 C.
Les particules élémentaires, constituant la matière, ont pour charges :
- l’électron : ;
- le proton : ;
- le neutron : sa charge est nulle.
L’unité de la charge est le coulomb C dans le SI. (MKSA).
4-3. Invariance de la charge électrique
Le principe de conservation de la charge est l’un des principes fondamentaux de conservation
qui sont à la base de la physique, tels que la conservation de l’énergie, de la quantité de
mouvement...
Il exprime que la charge électrique d'un système isolé est un invariant.

V. Loi de Coulomb
5-1. Enoncé de la loi de Coulomb
Considérons dans le vide, deux charges ponctuelles et , fixées en et respectivement.
Les deux charges stationnaires et exercent l’une sur l’autre une force proportionnelle à
chacune des deux charges et inversement proportionnelle au carré de la distance qui les sépare.
Ces deux forces électrostatiques sont dirigées suivant la droite qui lie les deux charges (Fig. 4).
Elles sont attractives si les deux charges sont de signes opposées (Fig. 4-a) ou répulsives
lorsqu’elles ont le même signe (Fig. 4-b).
Figure 4-a (
Figure 4-b (
La force
exercée par sur la charge s’écrit sous la forme :
Où r est la distance entre et , et
est le vecteur unitaire défini par :
est la permittivité du vide :
Conformément au principe de l’action et de la réaction, la force
exercée par sur la charge
est l’opposée de
:
Les forces
et
sont dirigées par la droite qui lie les deux charges et .

5-2. Analogie avec l’interaction de gravitation
Deux points matériels de masse et , placés respectivement en et exercent l’un sur
l’autre une force de gravitation. La force
exercée par sur est :
Figure 5
Où G est la constante de gravitation universelle.
La force de gravitation a la même formulation mathématique que la force électrostatique : elle
est dirigée suivant la droite qui lie les deux points matériels et et inversement
proportionnelle au carré de la distance qui sépare les deux points.
La force de gravitation joue un rôle fondamental dans la mécanique des objets macroscopiques
et dans la dynamique céleste. Cependant, à l’échelle atomique, cette force de gravitation est
négligeable.
A titre d’exemple, comparons la force de gravitation qui s’exerce entre l’électron et le proton
d’un atome d’hydrogène à la force électrostatique s’exerçant entre eux. La distance r qui sépare
l’électron de masse du proton de masse est environ
.
Comparons les deux forces :
m1
m2
r
 6
6
 7
7
1
/
7
100%