Exercice 2

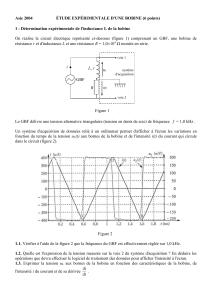
Exercice N°2
Un circuit électrique est constitué par l’association série d’un générateur de force
électromotrice E=6V, d’une bobine
d’inductance L et de résistance interne r, d’un résistor de résistance R0=100Ω et d’un
interrupteur K. Afin de visualiser simultanément les tensions u1 aux bornes du
générateur et la tension u2 aux bornes du résistor, on réalise les connexions adéquates
à un oscilloscope à mémoire comme l’indique la figure –a Sur l’écran de
l’oscilloscope on obtient l’oscillogramme du document-a
1°) Identifier, parmi les courbes C1 et C2, celle qui correspond à u2(t). Justifier.
2°)Montrer que l’intensité du courant électrique évolue de la même façon que u2.
3°)Le courant permanent ne s’établie pas instantanément dans le circuit.
a. Quel élément du circuit est responsable du retard de l’établissement du
courant?
b. Préciser le phénomène physique responsable de ce retard?

c. Montrer que la valeur de l’intensité I0 du courant lorsque le régime permanent s’établie est égale 0.05A
4°) En appliquant la loi des maille au circuit de la figure-a, Déterminer l’expression de l’intensité I0.En déduire la valeur
de r.
5°) a- Déterminer graphiquement la valeur de la constante de temps du circuit. Préciser sa définition.
b- Trouver la valeur de l’inductance L de la bobine.
6°)Sachant que i(t = 𝑬
𝑹 1-𝒆
− 𝒕
𝝉 ) avec R=R0+r. Trouver l’expression de la tension u3 de la bobine. Tracer son allure sur le
même document -a et préciser les points particuliers.
Exercice N°3
Partie I : Un circuit électrique comporte en série un générateur de tension de f.é.m. E=10V, un interrupteur (K), une
bobine (b1) d'inductance L1, et un résistor de résistance R = 80Ω. On se propose d'étudier l'évolution de l'intensité i du
courant qui s'établi dans le circuit à partir de l'instant t=0s de fermeture de (K).
1°) a- Quelle est la tension qu'on doit visualiser sur l'écran de l'oscilloscope pour réaliser cette étude? Justifier la réponse.
b- Préciser en le justifiant lequel parmi les montages de la figure (4-a) ou (4-b) , celui qui nous permet de réaliser cette
étude. c- En
utilisant les montages de l’annexe « figure (2-a) ou (2-b) « ajouter les connections nécessaires.
2°) Sur l'écran de l'oscilloscope on obtient la courbe de la figure -3- en annexe.
a-Etablir l'équation différentielle vérifiée par i(t).
b-Utiliser la courbe de la figure -3- pour montrer que la bobine est purement inductive.
c-Calculer l'intensité I0 du courant qui s'établit en régime permanant.
3°) a- Montrer que i(t) = I0 (1-𝒆
𝑹𝟏 𝒕
𝑳 ) est solution de l'équation différentielle
b- La constante de temps du dipôle R1L1 étudié est notée τ1, déterminer la valeur de i à l'instant t = τ1 et déduire
graphiquement la valeur de τ1.
c- Déterminer alors l'inductance L1 de la bobine (b1) du courant.
Partie II : On dispose du même générateur de l'interrupteur K, du même résistor R, d'une bobine (b2) de résistance r2 et
d'inductance L2.On veut visualiser la variation de la tension ub aux bornes de la bobine pendant l'établissement du courant
On réalise le montage avec la bobine (b1) et on ferme (K) puis on ouvre (K). on remplace (b1) par la bobine (b2) et on
réalise la même expérience. Sur la figure -5- on a représenté les courbes obtenues avec chacune des deux bobines lorsque
(K) est fermé.
1°)Faites correspondre chacune des deux courbes (A) et (B), à la bobine correspondante. Justifier la réponse.
2°) a- Choisir dans le tableau suivant et sans faire de calcul la valeur de l'inductance L2 de la bobine (b2). Justifier votre
choix
b- Etablir l'expression de la tension aux bornes de la bobine (b2) pendant le régime permanant "en fonction de : r2, R et E.
c- Déterminer alors la résistance r2 de (b2).
L2(H)
0,4
0,8
1,2

Exercice 3
On se propose d’étudier l’établissement du courant dans un dipôle série comportant une
bobine d’inductance L et une résistance r et un conducteur ohmique de résistance R0 =30 Ω
lorsque celui-ci est soumis à un échelon de tension de valeur E délivrée par un générateur
de tension idéal. Un oscilloscope à mémoire, est branché comme l’indique la figure 1,
permet d’enregistrer au cours du temps les valeurs des tensions.
1°) A l’instant t=0, on ferme l’interrupteur K, et on procède à l’enregistrement. On obtient les
courbes y1 =f(t) et y2=g(t) (figure 2).
a- Quelles sont les grandeurs électriques observées sur les voies A et B ?
Identifier y1 et y2. Justifier la réponse.
b- Quelle est la courbe qui permet de déduire la variation de l’intensité
de courant i au cours du temps ? Expliquer brièvement le comportement
électrique de la bobine.
c- Prélever du graphe la valeur de la force électromotrice du générateur.
2°) Lorsque le régime permanent est établi, l’intensité i prend la valeur
Ip, tandis que y2 prend la valeur Yp.
a- Donner, dans ces conditions, les expressions littérales des tensions
uAM, uAB et uBM.
Montrer, en utilisant les courbes de la figure 2, que la bobine a une résistance r non nulle.
b- Caculer :
 L’intensité IP.
 La résistance r de la bobine.
3°) Le circuit étudié peut être caractérisé par une constante de temps , qui permet d’évaluer la durée nécessaire à
l’établissement d’un régime permanent dans ce circuit. Pour un circuit (RL), on pose =L/R.
a- Montrer que  est homogène à un temps.
b- Que représente R dans le circuit étudié ? Quelle est sa valeur numérique ?
4°) On admet que, si i est l’intensité du courant dans le circuit à un instant t, alors : i=A(1-e-t/), montrer que A=IP.
5°) a- Déterminer graphiquement .
c- En déduire la valeur de l’inductance L de la bobine, et calculer l’énergie emmagasinée par celle-ci quand le régime
permanent est établi.
Exercice 4 :
On réalise le circuit électrique représenté par la figure 1 comportant , en série, un générateur de tension idéale de f.e.m
E,une bobine d’inductance L réglable et de résistance r=8 Ω,un interrupteur K et un résistor de résistance R0. A la date
t=0 on ferme l’interrupteur K et à l’aide d’un système d’acquisition approprié on enregistre la tension uB aux bornes de la
bobine, on obtient les chronogrammes 1 et 2 (figure 2) correspondant
respectivement à deux valeurs L1 et L2 de L.
1°) A l’aide de la loi des mailles, montrer que la tension aux bornes de la bobine
uB(0) à la date t=0 est égale à E. Déduire graphiquement la valeur de E.
2°) a- Comparer les constantes de temps 1 et 2 correspondant respectivement à
L1 et L2 . Comparer alors L1 et L2.
b- Sachant que L1=0,2 H, déduire, à partir du chronogramme, la valeur de L2.
3°) a- Etablir, en fonction de r, R0 et E ; l’expression de la tension aux bornes de
la bobine lorsque le régime permanent s’établit.
b- En utilisant le graphe, déterminer R0.
4°) a- Etablir l’équation différentielle régissant les variations, au
cours du temps, de la tension uB(t) aux bornes de la bobine
d’inductance L1. Montrer qu’elles’écrit sous la forme
duB
dt + uB
1 = rE
L1
b- La solution de cette équation différentielle est uB=Ae-t/1 + B.
Montrer que uB=R0I0e-t/1 + rI0.
R0
B
L,r
A
K
M
E
i
Fig 1
Fig 2
t
uB(V)
Courbe 1
Courbe 2

Exercice N°5: On réalise un circuit électrique AM comportant en série un conducteur ohmique de résistance
R=50 Ω, une bobine (B1) d’inductance L et de résistance supposée nulle et un interrupteur K. Le circuit AM est
alimenté par un générateur de tension de force électromotrice (f.e.m) E (fig 1). Un système d’acquisition adéquat
permet de suivre l’évolution au cours du temps des tensions uAM et uDM.
A l’instant t=0s, on ferme l’interrupteur K. Les courbes traduisant les variations de uAM(t) et uDM(t) sont celles de la figure 2.
1°) a- Montrer que la courbe 1 correspond à uDM(t).
b- Donner la valeur de la f.e.m du générateur.
2°) a- A l’instant t1=10 ms, déterminer graphiquement la valeur de la
tension uB1 aux bornes de la bobine (B1) et déduire la valeur de la
tension uR aux bornes du conducteur ohmique.
b- A l’instant t2=100 ms, montrer que l’intensité du courant électrique
qui s’établit dans le circuit électrique est I0=0,12 A.
3°) a- Déterminer graphiquement la valeur de la constante de temps
 du dipôle RL.
b- Sachant que = L/R, déterminer la valeur de l’inductance L de la
bobine (B1).
c- Calculer l’énergie emmagasinée dans la bobine en régime
permanent.
4°) On remplace la bobine (B1) par une bobine (B2) de même inductance L mais de résistance r non nulle. Les courbes traduisant
les variations de uAM(t) et uDM(t) sont celles de la figure 3
a- Montrer qu’en régime permanent, la tension aux bornes de la bobine (B2) est donnée par la relation uB2= r.E
R+r.
b- Déduire la valeur de la résistance r.
Exercice 6 test
Un circuit est composé d'un générateur de tension continue de f.é.m E, d'une bobine d'inductance L
et de résistance r, d'un interrupteur K , deux conducteurs ohmiques R0 et R' et une diode idéale. Les
bornes B, et M sont reliées aux entrées d’une carte d’acquisition. Voir document-5- Les entrées Y1,
Y2 et la masse de carte d’acquisition sont équivalentes respectivement aux entrées Y1, Y2 et à la
masse d'un oscilloscope .On donne: R0=200Ω et L=0,3H.
I/ Etablissement du courant dans un dipôle RL:
A un instant t = 0,on ferme l’interrupteur K.
1°) Quelles sont les tensions mesurées par la carte d’acquisition ?
2°) a- Etablir l’équation différentielle 𝐝𝐢
𝐝𝐭 +𝐢 𝛕𝟏 =𝐄 𝐋 avec 𝝉𝟏=𝑳 𝑹𝟏 et R1=R0+R’+r
b- Montrer que i(t)= 𝑬
𝑹𝟏( 1- e-t/ζ1) est une solution de l'équation différentielle précédente. Déduire l'expression de
l'intensité du courant I1 en régime permanent.
c- Montrer que uAM =E e-t/ζ1+ 𝒓
𝑹𝟏E( 1- e-t/ζ1) . Déduire son expression en régime permanent.
A
L
D
R
A
K
M
E
i
Fig 2
Fig 1
Courbe 1
Courbe 2
Fig
3

3°) Le système d'acquisition fourni les
courbes (1) et (2) du document-6-
a- Déterminer graphiquement :
- La f.é.m E ; La constante de temps ζ 1 du
dipôle R1L ; L’intensité du courant I1 en
régime permanent et La tension uAM aux
bornes de la bobine en régime permanent.
b- Déterminer r et R'.
II/ Annulation du courant dans un dipole RL:
A une nouvelle origine des temps t'=0s, on ouvre l’interrupteur K. Le système d'acquisition fourni les courbes (3) et (4)
du document-7-. représentants l’évolution de l’intensité du courant i en (mA) et de la tension uAM en (v).
1°) Montrer que la courbe(4) représente i=f(t).
2°) a- Calculer uMB aux bornes du conducteur Ohmique R0 à t=0s.
b- Déduire la tension uAM aux bornes de la bobine à t=0s.
3°) a- Donner l'expression de la constante de temps  0 du dipôle AB.
b- Comparer ζ 0 et ζ 1.
c- Déduire dans ces conditions, le phénomène le plus rapide; l'établissement ou l'annulation du courant dans le dipôle AB.
d- Quelle modification doit-on faire au circuit pour rendre l'établissement et l'annulation du courant
de même durée?(Proposer un schéma du circuit modifié).