Application (Chapter 3)
Exercise 1:
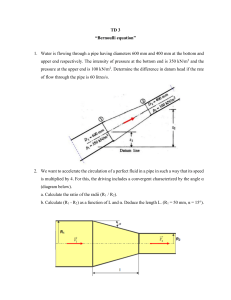
A venturi tube is arranged on an inclined water pipe. The pressure gauge connection tubes are
filled with water.
1) Calculate the difference in height of the pressure gauge as a function of V1, S1, S2,
water, m
2) Calculate the volume flow if = 90mm and D1 = 200mm and D2 = 90mm
Exercise 2:
We want to accelerate the circulation of a perfect fluid in a pipe so that its speed is
multiplied by 4. For this, the pipe has a convergent characterized by the angle α
(diagram above).
1) Calculate the ratio of the radii (R1 / R2). 2) Calculate (R1 - R2) as a function of L
and α. Deduce the length L. (R1 = 50 mm, α = 15 °)
Exercise 3: We consider a tank filled with water at a height H = 3 m, fitted with a
small orifice at its base with a diameter d = 10 mm. 1) By specifying the hypotheses
taken into account, apply Bernouilli's theorem to calculate the speed V2 of water flow.

2) Deduce the volume flow Qv in (l / s) at the outlet of the orifice. We assume that g =
9.81 m / s
Exercise 4: A perfect incompressible fluid flows from a circular orifice located on the side of
a tank with a volume flow qv = 0.4 L / s. The diameter of the hole is d = 10 mm. 1) Determine
the flow speed at the orifice. 2) State the theorem of Bernoulli. 3) How far from the free
surface is the hole? Exercise 5: We consider a cylindrical tank with an internal diameter D = 2
m filled with water up to a height H = 3 m. The bottom of the tank is provided with a hole of
diameter d = 10 mm allowing the water to drain out.
If a very small time dt is allowed to pass, the water level H of the reservoir drops
of an amount of H.

We notice:
the speed of descent of the water level, and V2 the speed of flow in the orifice.
We give the acceleration of gravity g = 9.81 m / s2. 1) Write the continuity equation. Deduce
the expression of V1 as a function of V2, D and d. 2) Write the Bernoulli equation. We
assume that the fluid is perfect and incompressible. 3) From the answers to questions 1) and
2) establish the expression of speed of flow V2 as a function of g, H, D and d. 4) Calculate the
speed V2. We assume that the diameter d is negligible in front of D. That is to say
.
5) Deduce the volume flow qV.
Exercise 6:

The cylindrical tank shown above, open to the air, has a section SA DA diameter = 2 m. It is
provided, at its base, with an emptying orifice of section SB and of diameter DB = 14 mm.
The tank is full up to a height H = (ZA - ZB) = 2.5 m of fuel oil, liquid considered as perfect
fluid, with density ρ = 817 kg / m3. We give - atmospheric pressure Patm = 1 bar. - the
acceleration of gravity g = 9.8 m / s2. We note α = (SB / SA) Part 1: The opening is closed by
a plug.
1) By applying the RFH, determine the pressure PB at point B.
2) Deduce the value of the pressure force FB which is exerted on the plug.
Part 2: The opening is open. The tank is emptied. The oil flows from the tank. Its average
flow velocity at point A is denoted VA, and its flow velocity at the level of the orifice is
denoted VB.
1) Write the continuity equation. Deduce VA as a function of VB and α.
2) By applying Bernoulli's theorem between A and B, establish the literal expression of the
speed VB as a function of g, H and α.
3) Calculate the value of α. The hypothesis of considering a level H of the fluid varies slowly
is it true? Justify your answer.
4) Calculate VB by considering the hypothesis that α << 1.
5) Determine the volume flow rate QV of the fluid flowing through the orifice. (in liter per
second)
6) What would be the duration T of the emptying if this flow remained constant?
1
/
4
100%