3

HAL Id: tel-01503037
https://tel.archives-ouvertes.fr/tel-01503037
Submitted on 6 Apr 2017
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-
entic research documents, whether they are pub-
lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destinée au dépôt et à la diusion de documents
scientiques de niveau recherche, publiés ou non,
émanant des établissements d’enseignement et de
recherche français ou étrangers, des laboratoires
publics ou privés.
Modélisation et instrumentation d’un bâtiment et de ses
systèmes pour optimiser sa gestion énergétique
Hugo Viot
To cite this version:
Hugo Viot. Modélisation et instrumentation d’un bâtiment et de ses systèmes pour optimiser sa
gestion énergétique. Autre [cond-mat.other]. Université de Bordeaux, 2016. Français. �NNT :
2016BORD0349�. �tel-01503037�

1
Thèse présentée pour obtenir le grade de
DOCTEUR DE L'UNIVERSITE DE BORDEAUX
Ecole Doctorale des Sciences Physiques et de l'Ingénieur
Spécialité : Mécanique
Par Hugo VIOT
Modélisation et instrumentation d'un bâtiment et de ses
systèmes pour optimiser sa gestion énergétique
Modeling and instrumentation of a building and its systems to optimize energy
management
Sous la direction de : Jean-Christophe BATSALE
et encadrée par : Alain SEMPEY, Laurent MORA
au sein du laboratoire I2M, UMR 5295, 33400 Talence
Soutenue en public le 29 novembre 2016
Membres du jury :
Christian INARD
Professeur des Universités (HDR), Université de La Rochelle
Président du jury
Benoit DELINCHANT
Maître de Conférences (HDR), Université de Grenoble
Rapporteur
Gilles FRAISSE
Professeur des Universités (HDR), Université Savoie Mont Blanc
Rapporteur
Jean-Christophe BATSALE
Professeur des Universités (HDR), ENSAM
Directeur de thèse
Alain SEMPEY
Maître de Conférences, Université de Bordeaux
Encadrant de thèse
Laurent MORA
Maître de Conférences, Université de Bordeaux
Encadrant de thèse

2

3
Résumé
Dans un contexte de raréfaction des énergies à bas coût et de lutte contre le changement climatique, le
secteur du bâtiment est contraint à des objectifs de diminution de ses consommations d'énergie. Un
contrôle adapté des systèmes énergétiques du bâtiment peut constituer un levier important pour tendre
vers cet objectif.
Le but premier de ces travaux est la construction de modèles de faibles dimensions afin de pouvoir les
embarquer dans un contrôleur pour améliorer la gestion énergétique. Ces modèles doivent être capables de
s’enrichir des mesures disponibles sur site. Un bâtiment démonstrateur situé à l'Institut Universitaire de
Technologie Génie Civil Construction Durable de Bordeaux sert de support au projet. Ce travail se décline
en quatre volets. Le premier concerne la modélisation puisque des modèles légers basés sur l'analogie
électrique et la représentation d'état sont proposés afin de décrire la dynamique du bâtiment sur un
horizon de contrôle de quelques jours. Le deuxième volet concerne l'instrumentation du bâtiment puisque
des campagnes de mesures courtes sont réalisées afin d'identifier les valeurs des paramètres du modèle de
façon à minimiser l'écart modèle-mesure. Certains capteurs servent par la suite pour la gestion
énergétique du bâtiment ; ces travaux posent donc également la question du jeu minimal de capteurs. Le
troisième volet concerne la caractérisation des systèmes servant à piloter l'ambiance puisque dans une
logique de contrôle optimal il faut être capable de relier l'effet de la commande sur la grandeur d'intérêt
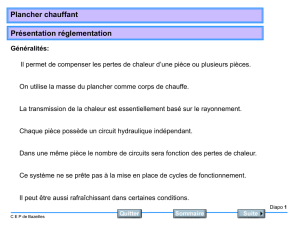
(température de confort). Le bâtiment démonstrateur comprend deux systèmes de chauffage : un plancher
chauffant et des ventilo-convecteurs ainsi qu'une centrale de traitement d'air double flux pour le
renouvellement d'air. Le dernier volet concerne la gestion énergétique avec l'utilisation d'un contrôleur
prédictif embarquant l'un des modèles identifiés.
Ainsi l’objectif est de chercher à anticiper le pilotage d'un système capacitif à long temps de réponse, tel
que le plancher chauffant, grâce à la connaissance des perturbations futures (occupation, météo) sur un
horizon de prédiction de quelques heures. Un contrôle réactif est assuré par les ventilo-convecteurs en
appoint. La gestion prédictive est comparée à des stratégies de gestion plus classiques en simulation et in
situ avec le bâtiment démonstrateur.
L'originalité de ces travaux est de proposer une démarche pour la mise en place d'une boucle de contrôle
complète (contrôleur/capteurs/actionneurs) et de montrer s'il existe un intérêt à la gestion prédictive de
systèmes à long temps de réponse dans le domaine du bâtiment.
Mots clés : bâtiments, modèles légers, identification, systèmes énergétiques, contrôle anticipatif.

4