Informatique : Langage Python
JFlottants : 3.14159,2.014e10,a+b,a*b ,a/b ,a**b (exponentiation), max(a,b),abs(a)
Remarque : Pour chaque nombre ‡ottant (en précision usuelle, dite double-précision), 52 bits sont utilisés pour stocker
la mantisse, 1 bit pour le signe et 11 bits pour la puissance, donc au total 64 bits (c’est-à-dire 8 octets).
JEntiers : a//b et a%b renvoient le quotient et le reste de apar b. Par exemple, n%2 == 0 ssi nest pair.
Si xest un ‡ottant, int(x) renvoie la partie entière de x(à distinguer de floor(x) qui renvoie un ‡ottant).
Il faut 1 octet (8 bits) pour stocker un entier compris compris entre 0et 255 = 281. Ainsi, une image 2D en 3 couleurs
(rgb) de taille 1000 1000 où l’intensité des couleurs est comprise entre 0 et 255 demande 3 MégaOctets.
JBooléens :True ,False (avec majuscules) , and , or , not , a==b , a!=b
Remarque : En Python, toutes les valeurs en tant que booléens valent True sauf la constante False,la constante None,
la constante 0, la liste vide [ ], le tuple vide ().Exemple :while L équivaut à while L != []
JIntervalles entiers : range(a,b,h) représente les entiers x=a+kh, avec kentier tel que x2[a; b[:
Par défaut, la valeur de hest 1;range(n) équivaut à range(0,n).
Exemple :for i in range(n) ; for i in range(n-1,-1,-1)
Listes
La structure de données la plus utilisée en Python est la liste. Les listes en Python sont des tableaux dynamiques.
JDé…nitions d’une liste : a = [1,2,3,’toto’]
JLongueur de la liste : len(a) renvoie la longueur nde la liste (c’est-à-dire le nombre d’éléments)
JListes dé…nies par compréhension :[ f(i) for i in range(n)]
JObtention d’un élément : a[i] renvoie l’élément d’indice idans la liste, pour 0in1:
Modi…er la valeur d’un élément : a[i] = a[i] + 1. Ces opérations se font en temps constant (en moyenne).
JAppartenance d’un élément à une liste :(x in a).
JConcaténation de deux listes : a+b, qui crée une nouvelle liste en O(n)opérations, où nlongueur de a
JPour dé…nir la liste acontenant nzéros : a = [0]*n ; a = [0]*n ; a = [0 for i in range(n)]
Opérations orientées-objets sur les listes !utilisation dans les procédures pour modi…er une liste
JA¤ectation des éléments : a[i] = ... , avec 0i < n, où nest la longueur de a.
JAjout d’un élément xà la …n de la liste a:a.append(x
JInsertion ou suppression d’un élément xen position i:a.insert(i,x), del a[i]
JSuppression et a¤ectation d’un élément : a.pop(i) supprime le i-ième élément et renvoie sa valeur.
La valeur par défaut de iest le dernier indice : a.pop() supprime le dernier élément de la liste.
Autres objets classiques en Python
JTuples : Le cas classique est celui des couples : (a,b) noté aussi a,b. De même les triplets (a,b,c), etc.
Les tuples ne sont pas mutables : On accède aux éléments comme pour les listes, mais on ne peut pas les modi…er.
L’a¤ectation directe par éléments est possible dans les tuples : (x,y,z) = (1,2,3)

Ainsi, pour échanger les valeurs de deux variables, il su¢ t donc de considérer : (x,y) = (y,x).
JChaînes de caractères (string) :
Chaîne de caractère : ’coco’ ou "coco" ;"c" représente un caractère ( = chaîne de longueur 1)
Remarque : En machine, un caractère est codé par un entier compris entre 0 et 255.
Longueur : len("coco") ; concaténation : "coco" + "rico"
Eléments d’une chaîne s:s[i] est le caractère d’indice i, par exemple "coco"[0] est le caractère "c"
Remarque : Contrairement aux listes, les caractères ne peuvent pas être modi…és (le type string est non mutable).
Modules ( = bibliothèques)
JUn module est en pratique un …chier Python contenant des dé…nitions de fonctions.
Par exemple la fonction logarithme log appartient au module “math”.
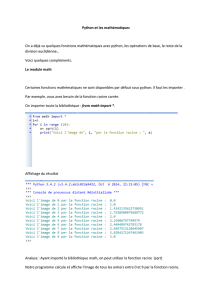
Pour charger le module “math” : import math. Ensuite, on peut utiliser la fonction math.log
Variante conseillée : from math import * . Ensuite, on utilise alors log directement au lieu de math.log.
Fonctions classiques : sqrt, sin, exp, log, abs, pi, floor et ceil (à valeurs ‡ottantes).
JModules courants :
from math import * # foncitons mathématiques
from scipy import * # calcul numérique
from numpy import * # calcul vectoriel, par exemple array
from matplotlib.pyplot import * # fonctions graphiques, par exemple plot
from random import randrange ; nombreAleatoire = randrange(1000)
JAttention : Dans la littérature, on utilise souvent la syntaxe suivante : import numpy as np
Ce qui permet ensuite d’utiliser l’abréviation np.array au lieu de numpy.array
Instructions de programmation
JLes instructions sont séparées par un point-virgule ou un passage à la ligne.
Dans un même bloc, deux instructions de même profondeur logique doivent avoir strictement la même indentation.
JA¤ectation des variables : L’a¤ectation se fait par le symbole =sous la forme variable = valeur
Attention à ne pas confondre =(a¤ectation) et == (symbole d’égalité dans les équations).
Par abréviation, on peut écrire x += a au lieu de x=x+a
Exemple important : L’échange de variables. La suite d’instructions z=x ; x=y; y=z permet d’échanger les valeurs
respectives de xet y:
En Python, pour les variables on peut opérer directement sur le couple (x; y)avec x,y = y,x
JInstruction conditionnelle IF
Syntaxe : if test1 : instructions1 elif test2 : instructions2 else : instructions3
Expression conditionnelle : expression1 if condition else expression2
JRépétitions inconditionnelles : boucles FOR

Syntaxe : for x in itérateur : instructions(x)
for i in range(len(a)) : instruction(i,l[a])
Remarque : L’instruction break au sein de la boucle provoque la sortie immédiate de la boucle. Elle est peu utilisée dans
les fonctions/procédures puique l’instruction return permet de sortir directement du corps de la fonction.
Types d’objets itérables : les intervalles range(1:4), les listes [1,2,3], chaînes de caractères , tuples,
Important : Listes dé…nies par extension à l’aide d’un itération : [ f(i) for i in range(0,n)]
JRépétitions inconditionnelles : boucles WHILE
Syntaxe : while test : instructions.
Evaluation paresseuse : i = 0 ; while i<=n-2 and a[i+1]==a[i] : ...
Dans cet exemple, le test a[i+1]==a[i]n’est e¤ectué que si i<=n-2 vaut True.
Fonctions et procédures
JSyntaxe :
def nom(arguments) :
corps_de_la_fonction
La valeur de retour d’une fonction est obtenue par l’instruction : return ... dans le corps de la fonction.
Remarque : L’instruction return remplace souvent des break dans les boucles for (au sein de fonctions)
JEn absence de return, la fonction renvoie la valeur None. C’est le cas généralement des procédures.
JVariables locales, variables globales : def f() : global s ; ...
L’utilisation d’une variable locale ayant même nom qu’un paramètre est déconseillée (pour raison de clarté).
JArguments par défaut : Une fonction peut être dé…nie avec davantage d’arguments qu’elle n’est utilisée. Dans ce cas,
les arguments supplémentaires doivent avoir une valeur par défaut. Exemple : def essai(x=1) ...
Tableaux (array)
JAvec le module numpy, on peut dé…nir et utiliser des tableaux (array).
JConstruction de tableaux (vecteurs et matrices) :
X = array([1,1,1]) ; Y = zeros(3) ; M = array([[1,2,3],[1,1,1]]) ; N = zeros((2,3))
Remarque : : M = array([[1,2,3],[1,1,1]]) dé…nit M=123
111:
JM.shape renvoie le couple (n; p)donnant respectivement les nombres de lignes et de colonnes.
Remarque : On pourrait aussi dé…nir n = len(M) et p = len(M[0]).
Jdot(M,X) renvoie le produit matriciel MX (produit de matrices ou de vecteurs).
Remarque : Sur les tableaux, les opérations s’e¤ectuent terme à terme (notamment l’addition +).
Ne pas confondre dot(M,M) avec M**2 (qui consiste à mettre au carré tous les coe¢ cients de M).
Conversions et copies
JLes fonctions int, float, str, list, array permettent de modifer le type d’un objet.

Exemple :a = int(3.2) renvoie la partie entière de 3.2 , c’est-à-dire l’entier 3.
Exemple :a = int(input"entrer un entier") ; en entrant la chaîne "2", on dé…nit l’entier a= 2:
Exemple :a = float(2) équivaut à a = 2.0 ;s = str(2) équivaut à s = "2"
Exemple : Pour dé…nir le tableau [0;1
5;2
5;3
5;4
5;1], on peut utiliser l’une des instructions suivantes :
from numpy import * ; array([i/5 for i in range(6)]) ;arange(0,6/5,1/5)
JLes commandes list et array permettent aussi de faire une copie (physique) des listes et tableaux :
Exemple :a = [1,2,3] ; b = list(a)
On peut aussi utiliser la méthode copy() :a = [1,1,1] ; b = a.copy() équivaut à b = list(a).
Représentations graphiques
from matplotlib.pyplot import * # bibliothèque graphique
La fonction de base est la fonction plot : Si xet ysont deux listes ou deux tableaux de même longueur n, l’instruction
plot(x,y) crée le graphe constitué de la ligne polygonale reliant les points (xk; yk)0k<n:
Exemple : On souhaite représenter dans [0;1][0;3] le graphe de la fonction y= exp(x)sur [0;1] par une ligne polygonale
composée de 100 segments correspondant à une subdivision régulière de [0;1] en 100 intervalles.
On dé…nit d’abord la liste xdes abscisses et la liste ydes ordonnées.
from math import exp
n = 10 ; x = [i/n for i in range(n+1)] # il y a donc n+ 1 points et nintervalles
y =[exp(i) for i in x]
plot(x,y,"ro-") # "r" pour rouge, "o" pour cercle et "-" pour tracer les lignes entre les points
axis ([0,1,0,3]) # on dé…nit ici les axes (contour du graphe), ici [0;1] [0;3]
show() # on représente le graphe dé…ni par les instructions précédentes.
Remarque : Par défaut, plot(x,y) équivaut à plot(x,y,"b-"), ce qui signi…e que les lignes sont représentées en bleu et
que les points de la ligne polygonale ne sont pas marqués.
Informatique : Algorithmique
1) Complexité
- En temps : Les opérations élémentaires sur les éléments des listes ou vecteurs se font en temps constant.
- En espace : Nombre de cases mémoires utilisées
Remarque : La réutilisation d’une même variable permet souvent de limiter l’espace mémoire. Par exemple, pour calculer
Xndé…nie par X0et Xk+1 =f(Xk), une seule case variable Xest nécessaire (ou deux si on ne peut pas calculer
directement Xk+1 à partir de Xksans utiliser une variable auxiliaire : on calcule à l’aide d’une variable auxiliaire Yla
nouvelle valeur de Xà partir de l’ancienne, puis on e¤ectue l’a¤ectation X=Y).
Remarque : On évalue parfois le nombre de bits utilisés (ou d’octets : 1 octet = 8 bits).
Mémoire vive (RAM), mémoire morte (ROM), exemple : 16 Go = 16 109octets.
2) Structures de données

- Listes (list) : structures dynamiques : L[len(L)-1] += 1 ; L.insert(i,x)
Notamment structure de piles : L.append(x) ; L.pop()
- Vecteurs (array) : la longueur est …xe ; possibilité d’opérations vectorielles.
3) Preuves de programmes
- Terminaison (pour les boucles while ou les programmes récursifs) :
On explicite une grandeur entière naturelle qui décroît strictement (principe de Fermat : il n’existe pas dans Nde suite
in…nie d’entiers strictement décroissante).
- Correction : On donne des invariants de boucles : on indique les valeurs des variables lors de la i-ième irération.
4) Méthodes de programmation
- Programmation récursive vs programmation impérative ( = itérative).
En programmation récursive, commencer par dé…nir le test d’arrêt.
En programmtion itérative, choisir for ou while selon que le nombre d’itérations est connu ou non.
- Programmation dynamique : stocker de l’information pour éviter d’e¤ectuer plusieurs fois les mêmes calculs.
- Utilisation de structures triées (selon un ordre judicieux) en traitement préliminaire pour optimiser la complexité.
5) Algorithmes de tris
- Tri en O(n2) : par sélection (on cherche le plus petit élément, puis le deuxième plus petit, etc), par insertions (on met
chaque élément à sa place …nale).
- Tri rapides par dichotomie en O(nlog n): tri fusion (pire cas en O(nlog n)) ; tri par pivot (O(nlog n)en moyenne si le
pivot est aléatoire, pire cas en O(n2) ; tri par insertions dichotomiques (en utilisant la structure dynamique des listes).
Remarque : Si les éléments à trier ne véri…ent pas de propriété particulière, le tri optimal est en O(nlog n):
5) Dichotomie
Remarque : Compte tenu des algorithmes proposés, la complexité c(n)est une fonction croissante de n.
-Exemple : Recherche d’un élément xdans une liste triée : En comparant xavec le médian (une opération), on se ramène
à la recherche de xdans des deux moitiés de liste. Notons c(n)le nombre de tests pour une liste de longueur n.
On a c(n)c(n
2)+1, d’où c(n) = O(log n):
En e¤et, si n= 2p, on a c(n)c(n
2)+1::: c(n2p) + p=c(1) + p.
Dans le cas général, avec 2p1< n 2p, on a c(n)c(2p)c(1) + p, avec p=dlog ne<1 + log n:
-Exemple : Tri rapide par fusion : c(n) = c(n
2) + c(n
2) + kn:
En e¤et, on coupe la liste en deux sous-listes, avec n
2+n
2=n:
On trie ces deux sous-listes, et on fusionne les listes triées en O(n)opérations.
On calcule d’abord la complexité dans le cas où n= 2p. On a alors c(n) = kn + 2c(n
2):
Donc c(n) = kn + 2kn
2+ 4c(n
4) = ::: =kn +kn +::: +kn + 2pc(n2p) = pkn + 2pc(1) = O(pn) = O(nlog n):
1
/
5
100%