autre lois

Autres LOIS de PROBABILITES
Professeur Pascale FRIANT-MICHEL
>Faculté de Pharmacie
[e-mail]

I - INTRODUCTION > II - LOI du x2 (1)
Les autres LOIS de PROBABILITES
Permet, en particulier, de comparer des distributions
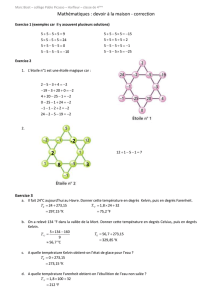
1. Définition
Soient X1, X2, . . . Xν, νlois normales centrées réduites N (0, 1)
indépendantes
II – LOI du χ2(lettre grecque : khi, on dit : loi du khi deux)
- Grand nombre de lois de probabilités
- Etude de trois lois très utilisées dans les tests statistiques
de formulation connue mais complexe
=> seules leurs principales caractéristiques seront données

II - LOI du χ2(2)
2. Propriétés
a) χ2∈ [ 0, + ∞ [
c) représentation graphique de la loi de χ2
b) distribution de χ2continue
. famille de courbes de χ2suivant le nombre νde degrés
de liberté
La loi de χ2à νdegrés de liberté est la loi de la variable
aléatoire somme :
χ2ν= + + . . . +
Remarque : χ2à 1 degré de liberté
est le carré d’une variable normale centrée réduite
. courbe en cloche unimodale asymétrique avec étalement
vers la droite (pour les faibles valeurs de ν)
?
X
1
2
?
X
2
2
?
Xν
2
1. Définition (2)