TD Transfert de matière

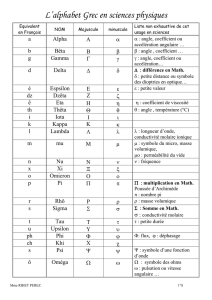
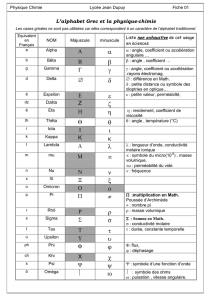
Université CADI AYYAD
Faculté des Sciences et Techniques de Marrakech
Travaux dirigés: Transfert de matière
M
odule : Génie des procédés
Année universitaire 201
7
-
2018

Exercice 1
- Donner l’expression de la densité du flux de diffusion et celle de la densité du flux de transfert
(système formé de i constituants).
- En déduire de cette expression que la somme des densités de flux de diffusion de ce système est égal
à zéro.
Calcul des coefficients de diffusion
Exercice 2
Considérons le système isobare et isotherme :
Un corps A volatil à l’état liquide, vaporisé dans un tube vertical initialement plein d’un gaz B.
1- Représenter le profil de x
A
le long du tube. (ne pas calculer x
A
).
2- Pour une fraction molaire x
A
= 1/6, la vitesse molaire moyenne V =12 cm/s, V
A
– V = 3 cm/s,
et la masse molaire de A M
A
= 5M
B
. Déterminer et représenter les différentes vitesses.
Exercice 3 Estimation du coefficient de diffusion d’un système binaire de gaz non-polaire
Partie 1 : Estimer le coefficient de diffusion pour un mélange méthane-éthane à 313 K et 136 atm en
utilisant l’équation de Bird.
Même question avec :
 P = 1 atm T = 140°C
 P = 0,1 atm T = 40°C
 P= 100 atm T = 40°C
Partie 2 : On donne la valeur D
AB
= 0,151 cm²/s pour le système CO
2
-air à 293K et une atmosphère.
Extrapoler D
AB
à T = 1500 K par la méthode de Bird.
Exercice 4 Estimation du coefficient de diffusion dans un mélange de gaz
Partie 1 : Le craquage de l’ammoniac sur une surface catalytique produit deux gaz: l’azote et l’hydrogène
selon la réaction suivante:
223
2
3
2
1HNNH +→
A une position donnée dans le réacteur où la pression est de 1 atm et la température est de 300K, le
mélange gazeux a la composition suivante : (1) 40% NH
3
, (2) 20% N
2
, et(3) 40% H
2
.
Estimer le coefficient de diffusion de l’ammoniac dans le mélange.
B
A
A
N
→

Craquage catalytique de NH
3
(N1) en N
2
(2) et H
2
(3)
Données :
Partie 2 : L’ammoniac se trouvant initialement dans un mélange de gaz stagnant (N
2
et H
2
) est absorbé
par une solution d’acide sulfurique. Estimer le coefficient de diffusion de l’ammoniac dans le mélange
gazeux, aux mêmes conditions citées dans la partie 1 (T, P, composition).
Exercice 5 Estimation du coefficient de diffusion dans une solution
Partie 1 : Estimer le coefficient de diffusion de l’éthanol dans une solution aqueuse (dilution infinie)
d’eau à T = 288K.
Donnée : µ
e
= 1,153 cP à T = 288 K
Partie 2 : Estimer le coefficient de diffusion de l’acide acétique (C
2
H
4
O
2
) dans une solution diluée
d’acétone (C
3
H
6
O) à T = 313 K.
Données : µ
acétone
= 0,264 cP à 313 K
Exercice 6 Détermination du coefficient de diffusion par la méthode Hartec dans le cas d’un mélange
gazeux
Dans ce problème, le constituant B diffuse vers A mais le phénomène de diffusion est
contrecarré par le mouvement d’ensemble du fluide à l’intérieur du capillaire.
σ
σσ
σ
(Å)
ε
εε
ε
/k (K)
M (g/mol)
NH
3
2,900
558,3
17
N
2
3,681
91,5
28,02
H
2
2,915
38,0
2,016
B
A
Echantillonnage
z = z
1
Tube capillaire
z = 0
Pompe maintenant la
pression constante
dans le mélangeur
V
Z

1- Identifier les données du problème et trouver une relation entre le coefficient de
diffusion de B dans A et ces données dans le cas où l’on suppose le régime permanent
établi.
2- Si Vz = 0, à quoi correspond l’établissement du régime permanent ?
3- Pour obtenir des mesures de concentration, prises au point d’échantillonnage, il est
parfois essentiel que les valeurs de ces concentrations appartiennent à un intervalle
assez restreint. Les coefficients de diffusion en phase gazeuse sont en général compris
entre 10
-2
et 1 cm²/s. Si le point d’observation se trouve au milieu du tube de longueur
de 20 cm, quelles valeurs doit-on choisir pour Vz si l’on désire obtenir : C
B
(z=z1)/C
B
(z=0) égal à :
a) 10
-3
b) 10
-2
c) 10
-1
d) 1
Etude du transfert de matière unidirectionnel en régime permanent
Exercice 7
On étudie la disparition d’un corps A réagissant sur une surface catalytique suivant une
polymérisation en phase gazeuse : nA (1)A
n
(2)
On suppose que la réaction est instantanée à la surface et que le phénomène n’est limité que
par la diffusion des molécules à travers un film stagnant d’épaisseurδ.
Nous prenons le cas où n = 2.
1- Donner la relation instantanée entre N1 et N2 par simple considération stœchiométrique.
2- Exprimer x
A
=f(z)
3- Etablir la relation donnant le flux de transfert de A. Calculer numériquement cette valeur.
Données : δ = 10
-4
m D
AA2
= 10
-5
m²/s P= 1 atm X
A0
= 0,8 T = 150°C
z =
δ
z = 0

Exercice 8 Diffusion à partir d’une goutte dans un gaz stagnant
Une goutte d’une substance A est suspendue dans un courant de gaz B stagnant. Le
rayon de la goutte est r
1
. Nous supposons qu’il existe un film sphérique de rayon r
2
entourant
la goutte. La fraction molaire de A dans la phase gazeuse est x
A1
à r = r
1
et x
A2
à r=r
2
.
1- Montrer que :
dr
dx
r
x
CD
Nr
A
A
AB
Ar 22 1
1
1
−
−=
avec N
Ar1
: le flux de matière de A à la surface de la goutte.
En déduire l’expression de N
Ar1
en fonction de r
1
, r
2
, D
AB
, x
B2
et x
B1
2- Si on définit kp comme coefficient de transfert de matière avec :
N
Ar1
= k
p
(p
A1
- p
A2
)
Montrer que quand r
2
∝ (cas de l’évaporation d’une goutte de liquide dans un grand
volume de gaz stagnant) :
( )
ml
B
AB
PD
CD
p
k
2
=
Où D est le diamètre de la goutte.
3- Montrer que dans le cas où la diffusion de A s’effectue dans un film non isotherme
pour lequel la variation de la température avec le rayon est donnée par :
n
r
r
T
T
=
11
et le coefficient de diffusion est donné par
2
3
11
=T
T
D
D
AB
AB
où D
AB
et
D
AB1
sont respectivement les coefficients de diffusion aux température T et T
1
:
a- L’équation de continuité relative au constituant A est donnée par :
Diffusion à travers un film gazeux isotherme
r
1
r
2
Goutte
Gaz B
T
1
T
2
=
T
1
(r
2
/ r
1
)
n