Electronique-Numerique EISTI Guy-Almouzni

Electronique Numérique 2007 - 2008
EISTI Guy Almouzni
ELECTRONIQUE
NUMERIQUE

Electronique Numérique 0. Préambule
0. 0
0. Préambule
ELECTRONIQUE NUMERIQUE
Différentes solutions électroniques :
. câblée : - avantage : rapidité - inconvénient : solution figée
. microprocesseur/microcontrôleur : - avantage : souplesse - inconvénient : lenteur/coût
. ordinateur embarqué : - avantage : souplesse - inconvénient : lenteur/coût
. FPGA (VHDL) : - avantage : souplesse - inconvénient : coût
Plan du cours
1. Logique combinatoire 1. Fonctions logiques combinatoires basiques. Technologie (1a.C + 1b.TD + 1c.TP)
- Algèbre de Boole
- Représentation des fonctions logiques
- Minimisation des fonctions logiques
- Matérialisation des fonctions logiques - Technologie
2. Logique combinatoire 2. Applications (2a.C + 2b.TD + 2c.TP)
- Les Applications directes (Codeur / Décodeur / Transcodeur / Multiplexeur / Démultiplexeur / Circuits arithmétiques)
- Les Réseaux Logiques Programmables (ROM / PROM / PAL-GAL / PLA-PLD / FGPA / RAM / ASIC)
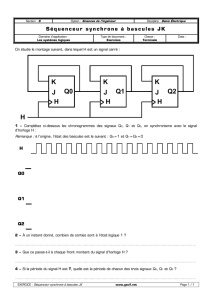
3. Logique séquentielle 1. Fonctions logiques séquentielles basiques (3a.C + 3b.TD + 3c.TP)
- Les bascules synchrones (RST /D /T / JK)
4. Logique séquentielle 2. Applications (4a.C + 4b.TD + 4c.TP)
- Registre
- Compteur
- Séquenceur
5. Le langage VHDL.
Le langage (6a.C + 6b.TD + 6c.TP)
- Eléments du langage / Unités de conception / Sous-programmes / Types de données / Déclarations & Spécifications / Instructions séquentielles /
Instructions concurrentes / Généricité / Attributs / Paquetage
Modélisation / Synthèse (7a.C + 7b.TD + 7c.TP)
- Modélisation (Registre & Additionneur / Cicuits linéaires / Automate d’étas finis / ALU / RAM / ROM)
- Synthèse (Circuits combinatoires / Circuits synchrones)
Annexe
6. Circuits Programmables.
7. Microprocesseur (5a.C + 5b.TD + 5c.TP/Exam)
- Matériel (Achitecture / Séquencement des instructions / ALU / Registres / Pile)
- Logiciel (Assembleur / Jeu d’instructions / Modes d’adressage / Adressage des périphériques / Interruptions)
- Interfaces
- Microcontrôleur (Achitecture / Système de développement / Familles de microcontrôleurs)
Annexe 1. Instructions VHDL
Annexe 2. Compilateur VHDL ALTERA Max+Plus
Annexe 3. Datasheets
8. Projet
. Cours (durée 1 h).
. TDs (durée 2 h).
. TPs (durée 2 h) : ils comportent une partie simulation ainsi qu’éventuellement une partie réalisation.

Electronique Numérique 0. Préambule
0.
1
Bibliographie
[1] R. Airiau & al. « VHDL langage, modélisation, synthèse » PPUR
[2] J. Auvray «
Electronique des signaux échantillonnés et numériques » Dunod
[3] G. Baudouin/F. Virolleau « Les processeurs de traitement de signal: famille 320C5X » Dunod
[4] B. Beghyn « Le microcontrôleur 68HC11 » Hermès
[5] Dietsche/Ohsmann « Manuel des microcontrôleurs 8032/805/80535 » Publitronic
[6] M. Gindre / D. Roux « Electronique numérique » McGraw-Hill
[7] R.D. Hersch « Informatique industrielle: microprocesseurs/temps réel » PPUR
[8] H. Lilen « Microprocesseurs : du CISC au RISC » Dunod
[9] E. Martin/J.L. Philippe « Ingénierie des systèmes à microprocesseurs » Masson
[10] M. Meaudre J. Weber « VHDL du langage au circuit, du circuit au langage » Masson
[11] B. Mitton « Interfaces et bus microprocesseurs 68000/68070 » Mentor sciences
[12] B. Mitton « Microprocesseur 68000 » Mentor sciences
[13] B. Odant « Microcontrôleurs 8051/8052» Dunod Tech
[14] C. Tavernier « Microcontrôleurs » Radio
[15] R.L. Tokheim « Les microprocesseurs » Série Schaum
PPUR : Presses Polytechniques et Universitaires Romandes
__________

Electronique Numérique 1. Logique combinatoire 1
1. 1
1. LOGIQUE COMBINATOIRE 1
0. Introduction
L’électronique logique (≡ électronique numérique) met en jeu des signaux binaires (n’ayant que 2 états possibles)
appelés bits et notés 0 (état logique bas) et 1 (état logique haut).
Système logique
pentrées msorties
p
Système Logique
sj
eim
1≤≤ip 1≤≤jm
Système logique combinatoire
A l’instant discret n, une sortie j s, notée sj
n, d’un système logique combinatoire ne dépend que de ses entrées
ee
n
p
n
1,..., au même instant : (la seule connaissance des entrées suffit à déterminer les sorties)
sfe e
j
nn
p
n
=( ,..., )
1 (1≤≤jm
)
Système Logique
Combinatoire
Entrées logiques Sorties logiques
p m
1≤≤ip 1≤≤jm
n
jj ss ≡
n
ii ee ≡
Système logique séquentiel
A l’instant discret n, une sortie sj
n d’un système logique séquentiel dépend de ses entrées ee
n
p
n
1,..., mais aussi de
l’état antérieur des sorties ( ss
n
m
n
1
11−−
,..., ) qui peuvent être considérées comme des entrées secondaires, alors que les
entrées ee
n
p
n
1,..., sont appelées primaires. (Notion de mémoire, car les systèmes séquentiels sont bouclés, ou encore
récursifs) : (la seule connaissance des entrées (primaires) ne suffit pas à déterminer l’état des sorties)
sfe es s
j
nn
p
nn
m
n
=−− ( ,..., , ,..., )
11
11
(1
≤
≤
jm
)
Système Logique
Séquentiel
Sorties logiques antérieures
Sorties logiques
Entrées logiques p
1≤≤ip 1≤≤jm
m1
m2
mm
1m2
+=
n
j
s
n
i
e
1−n
j
s
Logique combinatoire
1. Algèbre de Boole
1.1. Opérateurs Fondamentaux (ET, OU, NON)
En algèbre de Boole, une variable, ou une fonction, ne peut prendre que deux valeurs binaires que l'on note
symboliquement 0 et 1.
A l’aide de variables binaires (donc à 2 états) on peut néanmoins décrire des variables ayant un plus grand nombre
d’états, en constituant ces dernières comme des mots binaires. Un mot binaire est une association de variables binaires.
Ainsi un mot constitué de m bits ou variables binaires peut décrire 2m combinaisons logiques.
Ex: Mot binaire M formé de m= 3 variables logiques binaires aaa
210
,, →012 aaaM
=
peut prendre 23= 8
valeurs.

Electronique Numérique 1. Logique combinatoire 1
1. 2
On définit les opérateurs fondamentaux : (dans tout ce qui suit, x, a, b, c ... représentent des variables binaires (bits))
a) Le complément (≡ opérateur NON (NOT))
x
de x qui vaut 0 si 1
qui vaut 1 si 0
x
x
=
=
⎧
⎨
⎩
Un opérateur peut être associée à une représentation géométrique issue de la théorie des ensembles que l'on appelle
diagramme de Venn (ou d'Euler) :
a=1
a= 1
a= 1
b) La somme logique (≡ opérateur OU (OR)) de deux variables booléennes.
Cet opérateur est noté par le signe + (mais aussi par le signe ∨ ou encore ∪)
ab a b+=1si ou (ou les deux) vaut 1 et sinon0
=
+
ba . ab ab a b+≡∨
≡
∪
Le signe + n'a pas ici la signification habituelle, il est évident en effet qu'en algèbre de Boole : 1 + 1 = 1
Si une ambiguité peut exister, il vaut mieux alors utiliser la notation usuelle de la théorie des ensembles : ab
∪.
On considère un plan dans lequel on délimite une région où la variable a vaut 1 et une autre région dans laquelle b vaut
1. La somme logique a pour valeur 1 dans la surface formée par la réunion des deux régions précédentes :
a= 1 b= 1
a + b = 1
c) Le produit logique (≡ opérateur ET (AND)) de deux variables booléennes :
Cet opérateur est noté par le signe • (mais aussi par le signe
∧
ou encore
∩
ou même pas de signe)
baba etsi1=⋅ valent 1 et sinon0
=
⋅
ba . ab a b a b ab⋅≡∧≡
∩
≡
Le diagramme de Venn correspondant conduit à écrire ab
∩
:
a= 1 b= 1
= 1ab⋅