LoinormalecentreereduiteEXOSCORRIGES

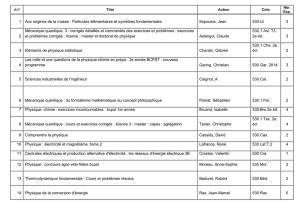
Loi N(0;1) - exercices corrigés
document disponible sur JGCUAZ.FR
LOI NORMALE CENTREE REDUITE
EXERCICES CORRIGES
Ce document totalement gratuit (disponible parmi bien d'autres sur la page JGCUAZ.FR rubrique
mathématiques) a été conçu pour aider tous ceux qui désirent travailler sur la loi normale centrée
réduite
Il contient 13 exercices corrigés intégralement, classés par thèmes et/ou par niveaux.
La page JGCUAZ.FR étant en constante évolution (ajout de nouveaux exercices, améliorations), il
est conseillé de régulièrement la visiter pour y télécharger la nouvelle version de ce fichier.
Pour toute remarque, merci de vous rendre sur la page JGCUAZ.FR où vous trouverez mon adresse
électronique (qui est [e-mail] à la date du 14/01/2018)
Egalement disponible une page facebook https://www.facebook.com/jgcuaz.fr
Montpellier, le 14/01/2018
Jean-Guillaume CUAZ,
professeur de mathématiques,
Lycée Clemenceau, Montpellier depuis 2013
Lycée Militaire de Saint-Cyr, de 2000 à 2013
Loi N(0;1) - exercices corrigés Page 1/13 version du 14/01/2018

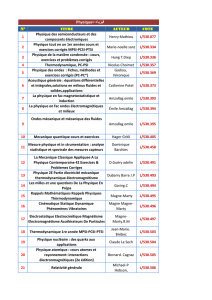
Loi N(0;1) - exercices corrigés
document disponible sur JGCUAZ.FR
LOI NORMALE CENTREE REDUITE - EXERCICES
Exercice n°1 (correction)
Une variable aléatoire X suit la loi normale centrée réduite N(0;1).
Donner l'arrondi au millième de :
a)
( )
0 1,3pX≤≤
b)
( )
2,1 0,4pX−≤≤
c)
( )
1, 6pX≤
d)
( )
0,5pX≥−
Exercice n°2 (correction)
Une variable aléatoire T suit la loi normale centrée réduite N(0;1).
Utiliser la courbe de la densité de cette loi pour expliquer pourquoi :
a)
( ) ( )
2,5 2,5pT pT≥− = ≤
b)
( ) ( )
1,5 0,5 0 1,5pT p T≤− = − ≤ ≤
Exercice n°3 (correction)
Une variable aléatoire T suit la loi normale centrée réduite N(0;1).
Tracer la courbe de f et représenter : a)
( )
1pT≤−
b)
()
13pT≤≤
c)
( )
2pT≥
Exercice n°4 (correction)
Lors d'une course à pied, le temps moyen mis par les participants a été de 3h.
On note T la variable aléatoire qui donne l'écart ,en heures,
3t−
où t est le temps mis par un
participant. On admet que T suit la loi normale N(0;1).
1) Que représente
( )
0,25pT≥
?
2) Calculer et donner l'arrondi au centième de :
a)
( )
0,25pT≥
b)
()
0,5pT≤−
c)
( )
0,1 0,2pT− ≤≤
Exercice n°5 (correction)
Une variable aléatoire T suit la loi normale centrée réduite N(0;1).
Dans chaque cas, déterminer l'arrondi au millième du nombre u tel que :
a)
( )
0,997puTu−≤ ≤ =
b)
( )
0,758pT u<=
c)
( )
0,4pT u≤=
d)
( )
0,25pT u>=
e)
( )
0,7pT u≥=
Loi N(0;1) - exercices corrigés Page 2/13 version du 14/01/2018

Loi N(0;1) - exercices corrigés
document disponible sur JGCUAZ.FR
Exercice n°6 (correction)
Une variable aléatoire T suit la loi normale centrée réduite N(0;1).
1) Calculer : a)
( )
1,96pT>
b)
( )
1,96pT<−
c)
( )
2,58pT>
d)
( )
1, 21 1,53pT− <<
2) Calculer le nombre réel u tel que : a)
( )
0,15
pT u<=
b)
( )
0,8pT u<=
Exercice n°7 (correction)
T est une variable aléatoire qui suit la loi normale centrée réduite et u est le nombre réel tel que :
( )
1 0,3p Tu−≤ ≤ =
1) Exprimer
( )
pT u≤
en fonction de
( )
1pT≤−
puis en déduire son arrondi au millième.
2) Déterminer l'arrondi au centième de la valeur u.
Exercice n°8 (correction)
T est une variable aléatoire qui suit la loi normale centrée réduite et v est le nombre réel tel que :
( )
0,2pT v≤=
1) Sans calcul, comparer v à 0. 2) Que vaut
( )
pT v≤−
?
Exercice n°9 (correction)
Lors d'un concours, la moyenne des notes est 8.
T est la variable aléatoire qui donne l'écart
8t−
où t est la note obtenue par un candidat.
T suit la loi normale centrée réduite N(0;1).
1) A combien faut-il fixer la note de réussite à ce concours pour que 60% des candidats soient
reçus? Donner l'arrondi de cette note au centième.
2) Dans quel intervalle de notes, centré en 8, se trouvent 80% des notes des candidats ?
Exercice n°10 (correction)
Une embouteilleuse remplit de jus de pommes des bouteilles de 100 cL.
On note T l'écart
100q−
, en cL, où q désigne la quantité de jus dans une bouteille.
On admet que T suit la loi normale N(0;1).
a) Déterminer l'arrondi au centième du nombre
0u>
tel que
( )
0,8puTu−≤ ≤ =
b) En déduire un encadrement, centré sur 100 cL, de la quantité de jus dans 80% des bouteilles.
Loi N(0;1) - exercices corrigés Page 3/13 version du 14/01/2018

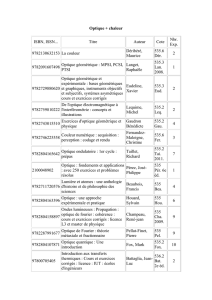
Loi N(0;1) - exercices corrigés
document disponible sur JGCUAZ.FR
Exercice n°11 (correction)
La température T relevée en janvier, en milieu de journée, suit la loi normale N(0;1).
a) Interpréter dans ce contexte, la valeur 0 de l'espérance de T.
b) Justifier que dans plus de 95% des cas, la température relevée est entre -2°C et 2°C.
c) Quelle est la fourchette de températures dans laquelle on trouve les températures relevées dans
99% des cas ?
d) Donner une estimation de la probabilité d'avoir un jour de janvier, une température supérieure à
2°C, puis vérifier à la calculatrice.
Exercice n°12 (correction)
Une boulangerie industrielle fabrique des baguettes dont la masse théorique est 200 g.
X est la variable aléatoire qui à une baguette associe sa masse en grammes.
On pose
200
4
X
Y− =
et on admet que Y suit la loi normale centrée réduite N(0;1).
Une baguette doit avoir une masse supérieure à 190 g pour être commercialisable.
On choisit une baguette au hasard dans la production.
1) Quelle est la probabilité que la baguette choisie au hasard ne soit pas commercialisable ?
2) Sachant que la baguette est commercialisable, quelle est la probabilité qu'elle pèse plus de 200g ?
Exercice n°13 (correction)
Lors d'une randonnée en montagne, la durée moyenne de parcours des 300 participants a été de 240
min.
X est la variable aléatoire qui à un marcheur associe la durée du parcours en minutes.
On pose
240
20
X
Y−
=
et on admet que Y suit la loi normale centrée réduite N(0;1).
1) Quelle est la probabilité qu'un marcheur choisi au hasard ait mis plus de 280 min pour faire cette
randonnée ?
2) Combien de personnes environ ont mis plus de 280 min pour faire cette randonnée ?
3) Déterminer le nombre réel t tel que la probabilité que la durée de parcours d'un marcheur soit
entre
( )
240 t−
et
( )
240 t+
minutes soit égale à 0,5.
Loi N(0;1) - exercices corrigés Page 4/13 version du 14/01/2018

Loi N(0;1) - exercices corrigés
document disponible sur JGCUAZ.FR
Exercice n°14 - d'après FESIC 2016 VRAI ou FAUX ? (correction)
Soit Y une variable aléatoire suivant la loi normale
( )
2
0;N σ
avec
0 σ >
Pour tout
u∈
, on pose
( ) ( )
u pY uΠ= ≤
( )
uΠ
représente l’aire de la surface hachurée ci-contre.
c.
( )
0 0,4pY σ ≤≤ >
d.
( )
1
10
σ Π− ≤
Loi N(0;1) - exercices corrigés Page 5/13 version du 14/01/2018