DS electronique 2019

OUAAQIL Mostafa
1
Lycée Omar Ibn Abdelaziz
CPGE – OUJDA DS de Physique
Durée : 2h
Les deux parties sont indépendantes.
PARTIE I :
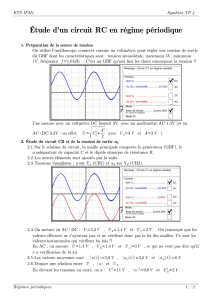
On considère un circuit RC série alimenté par un GBF qui délivre différents signaux de
fréquences et d’amplitudes réglables (voir fig.1)
1- Etablir l’équation différentielle qui relie  et .
2- En déduire que le circuit étudié est linéaire.
3- En analysant le comportement du condensateur à basse et à haute fréquence conclure
quant à la nature du filtre RC considéré
4- On donne  = a
Résoudre, en notation complexe, l’équation de la question 1 en écrivant  sous la forme
Exprimer alors A et  en fonction de a ,  , R et C.
5- En régime sinusoïdal forcé on définit, en notation complexe, la fonction de transfert
Ecrire  sous la forme  
 étant la fréquence du signal d’entrée.
Exprimer  et 
6- Définir et exprimer :
a- La fréquence de coupure  du filtre étudié.
b- Le déphasage Ѱ de  par rapport à .
7- Représenter le module de  en fonction de  en faisant apparaitre  sur le graphe.
8- On choisi  (en volt) avec =
a- Représenter le spéctre de 
b- Exprimer 
c- Simplifier cette expression sachant que  et 
d- En déduire, dans ce cas, la fonction mathématique réalisée par le circuit.
GBF
C
R
fig.1

OUAAQIL Mostafa
2
PARTIE II :
On considère le circuit RLC série de la figure 2.
1- Etablir l’expression de la fonction de transfert 
 et la mettre sous la forme :
Exprimer  et  en fonction de  et .
2- Représenter l’allure de la courbe . En déduire la nature du filtre étudié.
Dans la suite on supposera que  et 
 .
3- Montrer que le facteur de qualité  est lié à la bande passante  par la relation 
4- La tension d’entrée est triangulaire de valeur minimale , de valeur maximale  et
de fréquence  
On donne la décomposition en séries de Fourier de  :
a- Quelle est la valeur moyenne de  ?
b- Représenter le spectre de 
c- Tenant compte des valeurs numériques proposées, donner une expression approchée de 
et représenter son spectre.
d- On prend pour cette question .
i- En analysant la fonction de transfert prévoir le comportement du circuit à cette
fréquence.
ii- Représenter l’allure de  en précisant sa tension crête à crête.
GBF
C
fig.2
R
L

OUAAQIL Mostafa
3
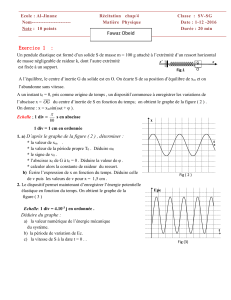
5- Bonus.
a- En analysant la fonction de transfert prévoir le comportement du circuit si .
b- Le signal d’entrée est toujours triangulaire (voir question 5-) mais de fréquence
. Analyser la courbe de  obtenue ci-dessous.