Jonction PN : Cours sur les Semiconducteurs

1
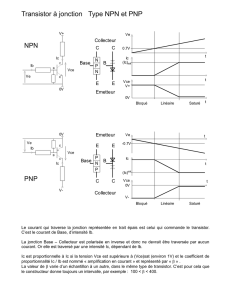
JONCTION PN
I) Notions sur les semiconducteurs
1) Les semiconducteurs
Comme leur nom le laisse entendre, les semiconducteurs occupent, sur l’échelle des
résistivités des matériaux solides, une position moyenne entre les métaux et les isolants.
Matériau
Métaux
Semiconducteurs
Isolant
Résistivité
10-6 cm
10-3 à 103 cm
108 cm
Dans les semiconducteurs la conduction électrique peut s’opérer :
 Soit par des électrons libres (matériau de type N)
 Soit par des trous libres (matériau de type P)
 Soit simultanément par électrons et trous libres
De même, dans les semiconducteurs, on peut moduler la concentration en électrons libres ou
en trous libres en diffusant dans le matériau certaines impuretés en quantité contrôlée. On a
donc le pouvoir de faire varier la conductivité.
a) Eléments semiconducteurs et semiconducteurs composés
Une très grande variété de matériaux sont semiconducteurs, en effet on peut construire
un matériau semiconducteur :
 Soit en assemblant des atomes de la colonne (IVa) du tableau de
classification périodique (Tableau de Mandéléieff). Exemple : le Silicium
et le Germanium qui sont des semiconducteurs bien connus, mais il faut
savoir que le carbone (sous sa forme diamant) et l’étain (sous sa forme
étain gris) sont également semiconducteurs.
 Soit en associant des éléments de la colonne (IIIa) et des atomes de la
colonne (Va) à raison d’un atome de la colonne (IIIa) pour un atome de la
colonne (Va), on réalise ainsi des semiconducteurs composés III-V.
Exemple : semiconducteurs binaires GaAs, GaP, InSb
Semiconducteur ternaire AlGaAs.
b) Arrangement des atomes dans les matériaux semiconducteurs
On va prendre comme exemple le Silicium. Le Silicium est l’élément de numéro
atomique 14, il possède donc 14 électrons disposés sur trois couches :

2
 Une couche K complète à deux électrons
 Une couche L complète à huit électrons
 Une couche M incomplète à quatre électrons
Dans un cristal de Silicium chaque atome est entouré de quatre atomes voisins, chaque
atome échange quatre liaisons de valence (une liaison de valence est obtenue par la mise en
commun de deux électrons, un électron par partenaire).
Cristal Silicium
Lorsque le matériau est dans l’état que nous venons de décrire à savoir les quatre
électrons de la couche périphérique d’un atome quelconque sont tous engagés dans des
liaisons de valence, il n’y a pas d’électrons libres, le matériau est parfaitement isolant
lorsqu’il est dans un état non excité (0K), on peut dire que le matériau est intrinsèque.
c) Semiconducteur intrinsèque
) Conduction électrique dans un semiconducteur
Lorsqu’on excite un matériau semiconducteur en le chauffant ou en l’éclairant par une
radiation lumineuse d’énergie suffisante, on peut alors briser des liaisons de valence, c'est-à-
dire arracher des électrons engagés dans ces liaisons. On crée alors simultanément et en
nombres égaux :
 Des électrons libres de charge –q (q=1,6.10-19 Coulomb)
 Des trous libres de charge +q

3
Si on applique au cristal un champ électrique, on observe :
 Un déplacement des électrons libres qui « remonte » le champ électrique
 Un déplacement « apparent » de l’ion Si+ qui « descend » le champ
électrique
Le transfert de la charge positive de l’atome 1 sur l’atome 2 puis sur l’atome 3 résulte
en fait du passage d’un électron lié à l’atome 2 sur l’atome 1, puis d’un électron lié à l’atome
3 sur l’atome 2.
Ainsi les semiconducteurs présentent deux types de conduction électrique, la
conduction par les électrons (comme dans les métaux) et la conduction par les trous libres
(liée au déplacement apparent des ions Si+).
  ) Résistivité d’un semiconducteur intrinsèque
La concentration en porteurs libres est le nombre de porteurs libres par unité de
volume.
On appellera :
 ni = concentration intrinsèque des électrons libres
 pi = concentration intrinsèque des trous libres
Ces concentrations varient selon la loi :
==3
2
2
Avec : T = température absolue (K)
Eg = énergie d’activation (J) (l’énergie qu’il faut pour activer un électron)
k = constante de Boltzmann (1,38.10-23 J/K)
A = coefficient dépendant du semiconducteur.
1
2
3
trou
Electron libre

4
Si on applique une différence de potentiel aux bornes d’un semiconducteur, la densité
de courant aura deux composantes, l’une est due au déplacement des électrons libres Jn=
nE
avec n=enni, l’autre due au déplacement des trous libres Jp=
pE avec p=e ppi.
Donc J= Jn + Jp = e(
nni + ppi)E
e(
nni + ppi) et =1
+
Cette résistivité varie comme l’inverse des concentrations en porteurs de charges est donc une
fonction décroissante de la température.
d) Semiconducteur extrinsèques
En lui-même le matériau intrinsèque que nous venons de voir ne présenterait que peu
d’intérêt pratique. On pourrait tout au plus en faire des thermistances ou des photorésistances.
Fort heureusement il est possible, en introduisant dans le matériau intrinsèque certaines
impuretés en quantité contrôlée afin de :
 Privilégier un type de conduction, conduction par électrons ou conduction
par trous.
 Contrôler la conductivité du matériau dans un large domaine.
 ) Semiconducteur extrinsèque de type N
L’insertion d’atomes pentavalents dans la structure cristalline d’un semiconducteur
permet d’introduire artificiellement des électrons libres, en effet un des cinq électron de la
couche périphérique des atomes pentavalents ne participe pas aux liaison covalentes. Au
voisinage de l’atome pentavalent, on trouve une charge positive l’atome est ionisé. Les
atomes pentavalents sont des atomes donneurs que l’on introduit dans le semiconducteur pour
le rendre extrinsèque de type N, ces atomes sont susceptibles de donner un électron libre, on
parle d’un dopage de type N.
Désignons par ND la concentration des atomes donneurs, par n celle des électrons
libres et par p celle des trous libres.
Comme le semiconducteur est électriquement neutre, le nombre des charges négatives
doit être égale au nombre des charges positives
n=p+ND
Atome ionisé
Charge positive fixe
Electron libre
Charge négative mobile

5
D’autre part, dans un semiconducteur extrinsèque de type N, les électrons libres sont
majoritaires et les trous minoritaires n>>p
n=ND=constante
Par ailleurs on démontre que le produit des concentrations en porteurs garde une
valeur constante, que le semiconducteur considéré soit intrinsèque ou extrinsèque, c’est la loi
de l’action et de masse :
n.p = ni.pi =ni2
p=ni2/ND
Il en résulte que la résistivité d’un semiconducteur extrinsèque de type N est de la forme :
=1
) Semiconducteur extrinsèque de type P
Dans le semiconducteur il est également possible d’introduire artificiellement des
trous plutôt que des électrons libres, il suffit d’insérer des atomes trivalents dans la structure
cristalline. Les électrons de la couche périphérique de ces atomes participent aux liaisons
covalentes laissant un trou dans la quatrième. Un électron quelconque peut quitter la liaison
qu’il occupe, laissant à son tour un trou derrière lui, et venir occuper la place vacante offerte
par l’atome trivalent. Tout se passe alors comme si le trou introduit était libre de se déplacer
dans le réseau cristallin. Au voisinage de l’atome trivalent, on trouve une charge négative
l’atome est ionisé. Les atomes trivalents sont des atomes accepteurs, introduits dans le
semiconducteur pour le rendre extrinsèque de type P. On parle ici d’un dopage de type P.
Désignons par NA la concentration des atomes accepteurs.
Comme le semiconducteur est électriquement neutre, le nombre des charges négatives
doit être égale au nombre des charges positives
p=n+NA
Atome ionisé
Charge négative fixe
Trou
Charge positive mobile