Manuel Sésamath 5e : Maths, Exercices et Compléments Numériques

Le Manuel Sésamath 5è est intégralement et librement accessible à tous sur Internet.
Il complète le manuel papier grâce à :
- des aides animées,
- des exercices interactifs,
- des liens pour aller plus loin : prolongements culturels, historiques, etc.
http://manuel.sesamath.net/
Navigation aisée à l’intérieur du manuel
et du chapitre
Liste des compléments numériques
(visible au survol d’un exercice)
Contenu du chapitre Diaporama exercice par exercice

NARRATIONS DE RECHERCHE...........................................................................9
TRAVAUX NUMÉRIQUES
N1 : PRIORITÉS, DISTRIBUTIVITÉ...............................................................13
N2 : NOMBRES EN ÉCRITURE FRACTIONNAIRE...............................................29
N3 : NOMBRES RELATIFS........................................................................43
N4 : CALCUL LITTÉRAL...........................................................................63
GESTION DE DONNÉES
D1 : PROPORTIONNALITÉ........................................................................77
D2 : STATISTIQUES...............................................................................91
TRAVAUX GÉOMÉTRIQUES
G1 : SYMÉTRIE CENTRALE.....................................................................103
G2 : TRIANGLES................................................................................117
G3 : PARALLÉLOGRAMMES....................................................................133
G4 : ANGLES....................................................................................149
G5 : PRISMES ET CYLINDRES.................................................................161
GRANDEURS ET MESURES
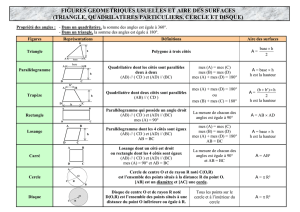
M1 : AIRES......................................................................................167
M2 : AIRES LATÉRALES ET VOLUMES........................................................179
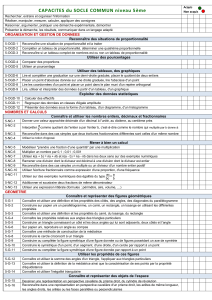
MÉTHODOLOGIE.......................................................................................187
CORRECTIONS DES « EXERCICES À TOI DE JOUER ».........................................190
PROPRIÉTÉS...........................................................................................197
LEXIQUE : L'ESSENTIEL DES NOTIONS............................................................203
FORMULAIRE...........................................................................................208
3

LISTE DES AUTEURS, RELECTEURS ET RÉDACTEURS DE COMPLÉMENTS
DE LA VERSION 2006 ET DE LA VERSION 2010
Nous remercions par ailleurs très chaleureusement les nombreux collègues ayant participé à la
rédaction des corrigés du manuel Sésamath 5e et à la création des compléments interactifs pour le
manuel numérique associé. La liste de ces participants, en constante évolution, est disponible sur le
site du manuel numérique.
UN PROJET COOPÉRATIF
4
Fr a nç ois e Cabuze l
Stéphane Dassonville
Sébas tien Dumoulard
Sébastien Hache
Isabelle Lemaître
Christophe Roland
Jean-Philippe Vanroyen
Laurent Charlemagne
Odile Guillon
Katia Hache
Laurent Hennequart
Emmanuel Ostenne
Boris Sissoeff
Gérard Vinot
Alexis Lecomte
Marc Mas s on
Sylvain Bourdalé
Sandrine Le Saint
Nathalie Gendre
Fr a n ço is Lo r ic
Thomas Crespin
Jean-Marc Gachas sin
Jos é Marion
Ya n n P o zza r
Anne Svirmickas
Rémi Angot
Xavier Birnie-Scott
Maxime Cambon
Audrey Chauvet
Emmanuel Chauvet
Benjamin Clerc
Sébas tien Cogez
Pierre-Yves Icard
Aline Meunier
Nicolas Moreau
Christian Payros
Isabelle Vivien
Laurent Zamo
Sandrine Baglieri
Fr a n ck G a ye
Gilles Bougon
Yolande Garous te
Sébastien Jolivet
Liouba Leroux
Xavier Ouvrard Brunet
Daniel Dehaese
Michel Souchet
Élisabeth Fritsch
Hervé Galliot
Denis Colin
Noël Debarle
Arnaud Rommens
Christophe Rindel
Rafael Lobato
Denis Bodet
Madeleine Abrahami
Michèle Badri
Alexandre Carret
Robert Corne
Rémi Deniaud
Hélène Dutang
Christophe Paumelle
Juliette Pelecq
Claudine Schwartz

UN PROJET DE
L'ASSOCIATION
SÉSAMATH
Le manuel Sésamath est un des projets de Sésamath. L'ensemble des
projets de l'association est consultable sur le site : http://www.sesamath.net/.
UN TRAVAIL
COLLABORATIF
Les échanges entre auteurs se font par listes de diffusion et via un wiki. Tous
les membres ont également accès à une interface collaborative sur Internet
qui permet de télécharger et de mettre en ligne les documents de travail du
manuel.
Le graphisme, la mise en page des documents et le contenu de chaque page
ont donc été l'objet de multiples discussions, relectures et améliorations.
UN TRAVAIL
LIBRE
L'association Sésamath étant attachée aux valeurs du logiciel libre,
le manuel Sésamath a été entièrement réalisé à l'aide de la suite
bureautique libre OpenOffice.org, téléchargeable gratuitement sur le site
http://www.openoffice.org/, ainsi que de l’éditeur d’équations Dmaths,
téléchargeable sur le site http://www.dmaths.org/.
L'ensemble du manuel est libre (licence GnuFDL 1.1) et téléchargeable
gratuitement sur le site http://manuel.sesamath.net/.
UN SITE RICHE
EN COMPLÉMENTS
Sur le site http://manuel.sesamath.net/, des compléments axés sur les TICE
(Technologies de l'Information et de la Communication pour l'Éducation) sont
disponibles gratuitement. Ces animations, réalisées par des enseignants, ont
nécessité l'utilisation de différents logiciels tels que :
•InstrumenPoche : http://instrumenpoche.sesamath.net/ ;
•Tra c e n Po ch e : http://tracenpoche.sesamath.net/.
L'utilisation du manuel peut aussi être prolongée par l'emploi :
•des cahiers Mathenpoche 5e : http://manuel.sesamath.net/ ;
•du logiciel Mathenpoche 5e : http://mathenpoche.sesamath.net/ ;
•du site Kidimath : http://kidimath.sesamath.net/.
AU-DELÀ
DE
SÉSAMATH
Ce projet n’a pu voir le jour que grâce à l’investissement de l’ensemble des
participants, qui ont bien souvent dû solliciter leur entourage pour mener leur
action à terme. Toute l’équipe du manuel les en remercie.
Nous remercions également tous les collègues qui nous ont apporté leur aide
via le site Sésaprof. Leur contribution et leurs relectures nous ont été très
utiles lors de la rédaction de ce manuel.
ILLUSTRATIONS
•Dominique Sénon
•Encyclopédie libre et gratuite Wikipédia : http://fr.wikipedia.org/.
UN PARTENARIAT
ÉDITORIAL
L'éditeur Génération 5 suit depuis plusieurs années l'association Sésamath
dans les différents projets qu'elle entreprend.
(Coordination éditoriale : Armelle Ronco)
UN PROJET COOPÉRATIF 5