Tp Acq 5

d2y(t)
dt + 2mωny(t)dy(t) dt +ω2
ny(t) = ω2 nx(t)
ωn
H(s) = ω2
n
s+ 2mωns+ω2
n
xiyi
yi=1
a0
Nb−1
X
j=0
bjxi−j−
Na−1
X
k=1
akyi−k
akk > 0
ak
z−1xi−1→x(z)z−1
x(t)y(t)
y(t) = dx
dt →yn=xn−xn−1 Te
H(z)H(s)
s1−z−1
Te
a0y(z) = b0x(z) + b1x(z)z−1+... +bNbx(z)z−Nb−a1y(z)z−1−a2y(z)z−2−... −aNay(z)z−Na
a0a1a2b0Tem ωn
a0a1a2b0

fc
m
fe

x(t) =
t
ˆ
0
y(t)dt →xn=xn−1+Te
2(yn+yn−1)
s→2(1 −z−1)
Te(1 + z−1)
H(z)H(s)
s2(1−z−1)
Te(1+z−1)

a0y(z) = b0x(z) + b1x(z)z−1+... +bNbx(z)z−Nb−a1y(z)z−1−a2y(z)z−2−... −aNay(z)z−Na
a0a1a2b0b1b2Tem ωn
∞
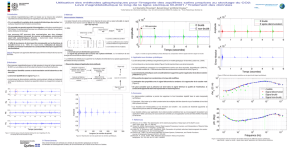
s+√2s+ 1
m=√2
20,707

e(t)
Cee(τ) = e(t)∗e∗(−t) = B0δ(τ)
s(t)h(t)
e(t)
s(t) = h(t)∗e(t)
Cse(t)
yk=
N
X
i=0
hixk−i