05 2nde p Chapitre 5 Refraction et dispersion de la lumiere
Telechargé par
samriikram

Chapitre 5 - Réfraction et dispersion de la lumière
BOUDIER Aurélien – 2nd B Page 1
I. Réfraction de la lumière
A. Mise en évidence expérimentale
1. Expérience
2. Observation
- Dans l’air et dans l’eau, la lumière se propage en ligne droite. C’est le phénomène de
propagation rectiligne de la lumière.
- Le faisceau lumineux change brusquement de direction lorsqu’il franchit la surface de
séparation AIR / EAU.
B. Le phénomène de réfraction
Lorsqu’on plonge une cuillère dans un verre d’eau, on peut observer qu’elle paraît cassée.
Comment expliquer ce phénomène ? Il s’agit du phénomène de réfraction !
La réfraction est le changement de direction que subit un rayon lumineux quand il
traverse la surface de deux milieux transparents différends. Un rayon perpendiculaire à la
surface n’est pas dévié.
Remarque :
Il existe aussi un rayon réfléchi (phénomène de réflexion lumineuse).
C. Les lois de la réfraction
1. Notations

Chapitre 5 - Réfraction et dispersion de la lumière
BOUDIER Aurélien – 2nd B Page 2
- La surface qui sépare deux milieux transparents différends est appelée le dioptre.
- Le milieu 1 est l’air et le milieu 2 est l’eau.
- Le rayon se propageant dans le milieu 1 est appelé le rayon incident.
- Le point I est le point d’intersection entre le rayon incident et le dioptre, il est également
appelé le point d’incidence.
- La droite perpendiculaire au dioptre passant par I est appelée la Normale, que l’on représente
en pointillé car c’est une ligne imaginaire.
- Le plan défini par le rayon incident et la normale au dioptre est appelé le plan d’incidence
(C’est le plan de la feuille dans notre cas).
- Le rayon se propageant dans le milieu 2 est appelé le rayon réfracté
- L’angle entre le rayon incident et la normale au dioptre est appelé angle d’incidence noté i1.
- L’angle entre le rayon réfracté et la normale au dioptre est appelé angle de réfraction noté i2.
Attention: Ne pas confondre rayon incident (ou rayon réfracté) avec l’angle d’incidence i1 (ou
l’angle réfracté i2).

Chapitre 5 - Réfraction et dispersion de la lumière
BOUDIER Aurélien – 2nd B Page 3
2. Enoncé des deux lois de Descartes
Première loi de Descartes :
Le rayon réfracté est dans le plan d’incidence.
Deuxième loi de Descartes :
L’angle d’incidence i1 et l’angle de réfraction i2 vérifient la relation suivante :
n1 . sin i1 = n2 . sin i2
n1 est l’indice de réfraction du milieu 1.
n2 est l’indice de réfraction du milieu 2.
L’indice de réfraction n caractérise un milieu transparent où n est un nombre sans unité,
supérieur ou égal à 1.
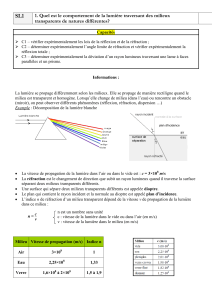
Indice de réfraction de différents milieux transparents :
Milieu
Indice (n)
Air, vide
1
Eau
1,33
Ethanol
1,36
Plexiglas
1,50
Verre
1,50
Diamant
2,42
(Ces mesures sont réalisées à l’aide d’un réfractomètre)
On a vu que c (célérité) est la vitesse de la lumière dans le vide, cela veut dire que dans un
milieu différent, celle-ci doit être différente, dans ce cas là on la note v.
L’indice d’un milieu est une grandeur sans unité, et la relation qui relie n, c, v est :
n = 𝐜
𝐯 ≥ 1
On sait que n = c
v donc n ≥ 1 car c est une vitesse limite dans l’univers et que l’on ne peut
donc pas dépasser. (Rappelons aussi que c est une constante qui vaut 3,0 x 108 m.s-1.)

Chapitre 5 - Réfraction et dispersion de la lumière
BOUDIER Aurélien – 2nd B Page 4
3. Conséquences : Etudes de trois cas
Cas n° 1 (Milieu 1 : AIR, Milieu 2 : EAU)
Selon la deuxième loi de Descartes,
n1 . sin i1 = n2 . sin i2
Milieu 1: AIR n1 = 1
Milieu 2: EAU n2 = 1,33
D’où, sin i1 = n2 . sin i2 (car n1 = 1)
On peut donc dire que : sin i1 sin i2 (sin i1 est en effet 1,33 fois plus grand que sin i2)
sin i1 sin i2
soit : i1 i2
Propriété : Quand un rayon arrive de l’air et se réfracte dans un milieu transparent
quelconque, il se rapproche de la normale

Chapitre 5 - Réfraction et dispersion de la lumière
BOUDIER Aurélien – 2nd B Page 5
Cas n° 2 (Milieu 1 : EAU, Milieu 2 : AIR)
Selon la deuxième loi de Descartes,
n1 . sin i1 = n2 . sin i2
Milieu 1: EAU n1 = 1,33
Milieu 2: AIR n2 = 1
D’où, sin i2 = n1 . sin i1 (car n2 = 1)
On peut donc dire que : sin i2 sin i1 (sin i2 est en effet 1,33 fois plus grand que sin i1)
sin i2 sin i1
soit : i2 i1
Propriété: Quand un rayon arrive d’un milieu transparent quelconque et se réfracte dans
l’air, le rayon réfracté s’éloigne de la normale.
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
1
/
13
100%