5 - Détection Contours

Traitement d’images
Détection de contours

2
Introduction
Rôle de la détection de contours en vision
1- Réduction d’information
•Information de toute l’image résumée dans le contours des différents objets.
•Contours : parties les plus informatives d’une image.
2- Etape souvent nécessaire à l’extraction d’autres primitives notamment
géométriques : droites, segments, cercles
Détection de contours : applications
1- Reconnaissance d’objets, de formes, classifications de scènes
2- Mise en correspondance stéréoscopique: calibration, reconstruction 3D
3- Compression d’images

3
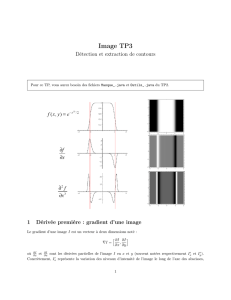
La détection de contours est une technique de réduction d'information dans les
images, qui consiste àtransformer l'image en un ensemble de courbes,pas
forcément fermées, formant les frontières significatives de l'image.
Introduction

4
Plan du cours
1. Modélisation des contours
•Notion de contour
• Caractérisation des points contours
•Rappel sur le gradient (dérivée première)
•Utilisation des dérivées secondes
2. Approches basées filtrage
•Filtrage du premier ordre
•Filtrage du second ordre
3. De l’image dérivée aux contours
•Seuillage

5
Notion de contour
Contour : frontière qui sépare deux objets (ou un objet du fond) dans une image
Caractérisation des zones de contours
variation brusque d’intensité de l’image
discontinuité de l’image