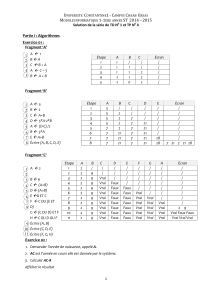
Introduction à l’algorithmique
L1 MPCIE
Organisation du cours
Cours / TD : 35h
- 2 Cours d'1h20 par semaine
TP : 20h
- 9 TP de 2h + 1 contrôle TP, à partir de la deuxième semaine (bâtiment G, 1er étage)
- Apporter son cours en TP
- Se munir d'une clef USB pour sauvegarder votre travail à la fin de chaque TP
- Travail sur machine en dehors des TP conseillé
Évaluation
- 2 contrôles continus communs ("CCC") : CCC1 vers la Toussaint, CCC2 fin décembre
- 1 contrôle continu TP ("CCTP") en décembre
- 1 note de TD ("CCTD") calculée à partir d'au moins deux contrôles continus TD
- Coefficients : CCC1 x2 ; CCC2 x2 ; CCTP x1 ; CCTD x1
Études en informatique à l'université d'Angers
Discipline informatique
Théorique
analyse numérique, théorie de l'information, théorie des langages, automates, …
Scientifique
résolution de problèmes complexes, bio-informatique, cryptologie, intelligence artificielle, …
Méthodologique
analyse, langages, génie logiciel, …
Technologique
composants, mémoires, périphériques, …
Systèmes
architecture, réseaux, systèmes d'exploitation, …
Applications
informatique de gestion, bureautique, conception assistée par ordinateur, automatique, robotique,
informatique médicale, GPS, internet, jeux vidéo, …
Discipline informatique
ENIAC, 1945
30 tonnes, 160 m² au sol, 5000 additions par seconde 2010-2020
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
1
/
61
100%
