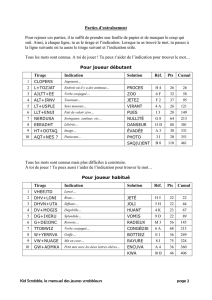
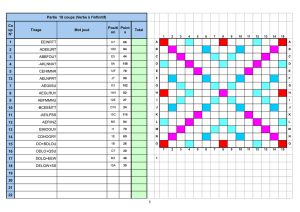
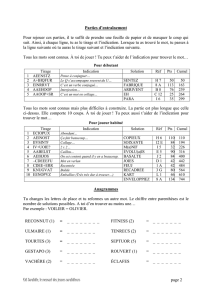
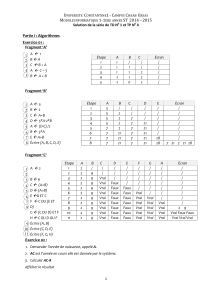
Exercice supplémentaire de probabilité en Turbo Pascal

Exercice suppl´ementaire de probabilit´e en Turbo Pascal
EDHEC 2004 Exercice 3 :
On d´esigne par nun entier naturel sup´erieur ou ´egal `a 2.
On lance n fois une pi`ece ´equilibr´ee (c’est-`a-dire donnant ”pile” avec la probabilit´e 1
2et ” face” ´egalement avec la
probabilit´e 1
2), les lancers ´etant suppos´es ind´ependants.
On note Zla variable al´eatoire qui vaut 0 si l’on n’obtient aucun ”pile” pendant ces nlancers et qui, dans le cas
contraire, prend pour valeur le rang du premier ” pile”.
1. (a) D´eterminer, en argumentant soigneusement, l’ensemble Z(Ω).
(b) Pour tout kde Z(Ω), calculer P(Z=k). On distinguera les cas k= 0 et k>1.
(c) V´erifier que P
k∈Z(Ω)
P(Z=k) = 1.
(d) On rappelle que l’instruction ”random(2)” renvoie un nombre au hasard parmi les nombres 0 et 1. Recopier
et compl´eter le programme suivant pour qu’il simule l’exp´erience d´ecrite ci-dessus, l’entier n ´etant entr´e au
clavier par l’utilisateur (“pile” sera cod´e par le nombre 1 et “face” par 0).
Program EDHEC2004 ;
var k, n, z, lancer : integer ;
Begin
Randomize ;
Readln(n) ; k : = 0 ; z : = 0 ;
Repeat
k : = k + 1 ; lancer : = random(2) ;
If (lancer = 1) then .................. ;
until (lancer = 1) or.......... ;
Writeln (z) ;
end.
Dor´enavant, on dispose de n+ 1 urnes U0, U1, ..., Untelles que pour tout kde {0,1, ..., n}, l’urne Ukcontient k
boules blanches et n−kboules noires.
On effectue des tirages d’une boule, au hasard et avec remise dans ces urnes de la fa¸con suivante :
si apr`es les lancers de la pi`ece d´ecrits dans la premi`ere question, la variable Zprend la valeur k(avec k>1),
alors on tire une par une et avec remise, kboules dans l’urne Uket l’on note Xla variable al´eatoire ´egale au
nombre de boules blanches obtenues `a l’issue de ces tirages.
Si la variable Za pris la valeur 0, aucun tirage n’est effectu´e et Xprend la valeur 0.
2. D´eterminer X(Ω).
3. Compl´eter le programme Turbo-Pascal pr´ec´edent, afin qu’il simule la variable al´eatoire X.
4. (a) D´eterminer, en distinguant les cas i= 0 et 1 6i6n, la probabilit´e P(X=i/Z = 0).
(b) D´eterminer, en distinguant les cas i=net 0 6i6n−1, la probabilit´e P(X=i/Z =n).
(c) Pour tout kde {1,2, ..., n −1}d´eterminer, en distinguant les cas 0 6i6ket k < i 6n, la probabilit´e
conditionnelle P(X=i/Z =k).
5. (a) Montrer que P(X= 0) =
n−1
P
k=1
(n−k
2n)k+1 2n.
(b) Montrer que P(X=n) = 1
2n.
(c) Exprimer, pour tout ide {1,2, ..., n −1},P(X=i) sous forme d’une somme que l’on ne cherchera pas `a
r´eduire.
6. V´erifier, avec les expressions trouv´ees `a la question pr´ec´edente, que
n
P
i=0
P(X=i) = 1.

Corrig´e de la partie informatique :
La partie en gras, correspond aux rajouts demand´es.
Question 1.d)
Program EDHEC2004 ;
var k, n, z, lancer : integer ;
Begin
Randomize ;
Readln(n) ; k : = 0 ; z : = 0 ;
Repeat
k : = k + 1 ; lancer : = random(2) ;
If (lancer = 1) then z :=k ;
until (lancer = 1) or (k=n) ;
Writeln (z) ;
End ;
Question 3.
Program EDHEC2004 ;
var k, n, z, lancer : integer ; i, x :integer ; tirage :real ;
Begin
Randomize ;
Readln(n) ; k : = 0 ; z : = 0 ;
Repeat
k : = k + 1 ; lancer : = random(2) ;
If (lancer = 1) then z :=k ;
until (lancer = 1) or (k=n) ;
Writeln (z) ;
x :=0 ;
For i :=1 to z do
Begin
tirage :=random ;
If tirage <= z/n then x :=x+1 ;
End ;
write(’X= ’,x) ;
end.
Variante :
tirage :=random(n)+1 ;
If tirage <=z then x :=x+1 ;
....
Cette variante demande alors que la variable tirage soit d´eclar´ee comme un entier.