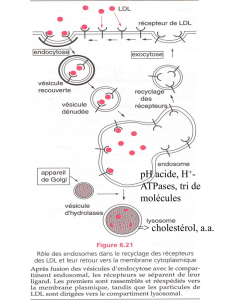
Télécharger

CORRECTION DM n˚9
PROBLÈME - Interpol enquête
Partie I - Le criminel commet une bourde
ņ
1. On note P
k 0
(a) Si ϕpP q
ņ
pk X k , on a donc ϕpP q pk pX qk
k 0
P
alors on a l’égalité P pX q
que P est une fonction paire.
P pX q soit @x P R, P pxq P pxq ainsi cela signifie
Réciproquement, si @x P R, P pxq P pxq, alors @x P R, P pxq P pxq 0.
Ainsi le polynôme associé ϕpP q P admet tout nombre réel comme racine, c’est donc le polynôme
nul c-à-d ϕpP q P .
(b) Notons P
ņ
pk X k
k 0
On a aussi ϕpP q ¸
t
¸
t
n
u
2
t
p2k X 2k
k 0
n
u
2
¸
n
u
2
p2k X
2k
k 0
¸
t
1X
2k 1
.
k 0
n
u
2
p2k
p2k
k 0
L’égalité ϕpP q P équivaut alors à 2
1X
¸
2k 1
.
n
u
2
t
p2k
1X
2k 1
0 soit @k P N, p2k 1 0.
k 0
On a donc bien P est paire si, et seulement si, @k
2. (a)
P N, p2k 1 0.
Si ϕpP q P alors on a l’égalité P pX q P pX q soit @x P R, P pxq P pxq ainsi cela
signifie que P est une fonction impaire.
Réciproquement, si @x P R, P pxq P pxq, alors @x P R, P pxq P pxq 0.
Ainsi le polynôme associé ϕpP q P admet tout nombre réel comme racine, c’est donc le polynôme
nul c-à-d ϕpP q P .
(b) P
¸
t
n
u
2
k 0
¸
t
p2k X
2k
n
u
2
p2k
1X
2k 1
et ϕpP q k 0
L’égalité ϕpP q P équivaut alors à 2
¸
t
n
u
2
¸
t
n
u
2
p2k X
k 0
p2k X 2k
2k
¸
t
n
u
2
p2k
1X
2k 1
.
k 0
0 soit @k P N, p2k 0.
k 0
On a donc bien P est impaire si, et seulement si, @k
P N, p2k 0.
Partie II - Les méthodes de la police locale divisent
1. F est un sous-ensemble de RrX s.
On montre très facilement que F est stable par combinaison linéaire et contient l’élément neutre.
2. Soit P P F .
P p1q P 1 p1q 0 ô pX 1q2 |P (1 est racine double de P ).
P p1q P 1 p1q 0 ô pX 1q2 |P (1 est racine double de P ).
Ainsi P P F si, et seulement si, pX 1q2 |P et pX 1q2 |P soit pX 2 1q2 |P .
3. (a)
Fn étant défini comme l’intersection de deux sous-espaces vectoriels , c’est un s.e.v. de RrX s.
€ RnrX s par définition donc Fn est nécessairement de dimension finie et dim Fn ¤ n 1.
Ici 0 ¤ n ¤ 3. Soit P P Fn alors deg P ¤ 3 et pX 2 1q2 |P .
La relation de divisibilité implique deg P ¥ 4 ce qui est impossible sauf si P est le polynôme nul.
Finalement Fn t0u et donc dim Fn 0.
Soit i P rr0, n 4ss et Li X i pX 2 1q2 .
Remarquons que la famille pLi qiPrr0,n4ss est échelonnée (degpLi q i 4) donc libre.
F
(b)
(c)
Lycée de l’Essouriau - Les Ulis
1
PCSI
CORRECTION DM n˚9
De plus pour i P rr0, n 4ss, Li appartient à F d’après le 2. et degpLi q ¤ n donc Li
On en déduit que pLi qiPrr0,n4ss est une famille libre de Fn .
P RnrX s.
Montrons que la famille est génératrice :
n¸
4
P Fn, DQ P Rn4rX s tel que P pX 2 1q2Q avec Q aiX i.
i0
n¸
4
n¸
4
ai Li et la famille pLi qiPrr0,n4ss est génératrice.
ai pX 2 1q2 X i On a donc P Soit P
i 0
i 0
On en conclut que c’est une base de Fn et donc dimpFn q n 3 .
Partie III - Interpol en alerte. Un ermite suspect en fuite
1. Procédons par double implication.
Supposons que Q P Ωα ô Qp1q Qp1q 0 et Q1 p1q Q1 p1q α.
Comme P P Ωα alors P p1q P p1q 0 et P 1 p1q P 1 p1q α.
Ainsi on obtient pQ P qp1q Qp1q P p1q 0 0 0 et pQ P qp1q Qp1q P p1q 0 0 0.
De même pQ P q1 p1q Q1 p1q P 1 p1q α α 0 et pQ P q1 p1q Q1 p1q P 1 p1q α α 0.
Soit Q P P F .
Réciproquement, si Q P P F alors Qp1q P p1q 0 soit Qp1q 0 et de même Qp1q 0.
De même Q1 p1q P 1 p1q 0 soit Q1 p1q α et de même Q1 p1q α.
Finalement Q P Ωα .
2. Q P Ωα ô Q P P F (d’après la question précédente)
Q P Ωα ô pX 2 1q2 |Q P (d’après le II.2.)
Q P Ωα ô DQ1 P RrX s, Q P pX 2 1q2 Q1 pX q soit QpX q P pX q
pX 2 1q2Q1pX q
3. Soit Q P Ωα , posons RpX q QpX q. On a trivialement Rp1q Qp1q 0 et Rp1q Qp1q 0.
Remarquons que R1 pX q Q1 pX q donc R1 p1q Q1 p1q α et R1 p1q Q1 p1q α et finalement
R P Ωα .
4. P P Ωα donc l’ensemble est non vide. Soit Q P Ωα de degré inférieur ou égal à 3.
D’après le 2., DQ1 P RrX s, QpX q P pX q pX 2 1q2 Q1 pX q mais comme deg Q 4 alors Q1 0
nécessairement.
Posons la division euclidienne de P pX q par pX 2 1q2 , il existe alors un unique couple pQ2 , P0 q P RrX s2
avec deg P0 4 tel que QpX q P pX q P0 pX q Q2 pX qpX 2 1q2 .
Comme deg Q 4 alors Q2 0 nécessairement et Q P0 .
Finalement si P0 existe, le seul qui convient est le reste P0 de la division euclidienne de P par pX 2 1q2 .
Reste à vérifier si ce reste est bien dans Ωα mais la relation P pX q P0 pX q Q2 pX qpX 2 1q2 s’écrit
aussi P0 pX q P pX qQ2 pX qpX 2 1q2 et d’après le 2. ceci prouve que P0 est bien un élément de Ωα .
5. P0 p1q P0 p1q 0 prouve que 1 et
1 sont racines de P0 donc que pX 2 1q|P0 soit :
P0 pX 2 1qpaX bq
D’après le 3., P0 pX q appartient également à Ωα mais comme ce polynôme est aussi de degré inférieur
ou égal à 3, par unicité on en déduit que P0 pX q P0 pX q et donc que P0 est impair, soit b 0.
Finalement on a P0 aX pX 2 1q avec a P R.
aX pX 2 1q aX 3 aX donc P01 3aX 2 a.
Les conditions P01 p1q P01 p1q α donnent 2a α soit a α2 soit P0 α2 X pX 2 1q.
Trivialement en utilisant la question 2. et en choisissant P P0 on obtient :
α
Ωα t X pX 2 1q QpX qpX 2 1q2 | Q P RrX su.
2
6. P0
7.
Autrement dit, il s’agit de l’ensemble des polynômes dont le reste dans la division euclidienne par
pX 2 1q2 est α2 X pX 2 1q.
Lycée de l’Essouriau - Les Ulis
2
PCSI
CORRECTION DM n˚9
Partie IV - Le fugitif barricadé dans la grange
1.
La base canonique de Rn rX s est p1, X, X 2 , . . . , X n q et sa dimension est de n
1.
2. Montrons que G contient le neutre et qu’il est stable par combinaison linéaire.
Soit P0 le polynôme nul, alors @i P rr1, n 1ss, P0 pαi q 0 et donc :
pP0pα1q, . . . , P0pαn 1qq p0, . . . , 0q P G
Soit deux éléments u et v de G, λ et µ deux réels. Il existe deux polynômes P et Q tels que :
u pP pα1 q, . . . , P pαn
pQpα1q, . . . , Qpαn 1qq
Alors λu µv pλP pα1 q µP pα1 q, . . . , λP pαn 1 q µP pαn 1 qq.
En posant R λP µQ qui est un polynôme, on en déduit que λu µv pRpα1 q, . . . , Rpαn 1 qq P G.
Finalement G est bien un s.e.v. de Rn
3. Soit u P G, DP
u
ai X i
ņ
ai α1i , . . . ,
i 0
qq
et v
1.
P RnrX s tel que u pP pα1q, . . . , P pαn 1qq donc :
i 0
ņ
ņ
1
ai αni 1
i 0
ņ
ai pα1i , . . . , αni
i 0
On en déduit que la famille p~g1 , . . . , ~gn
1
¸
n 1
aj ~gj
¸
n 1
aj pα1j 1 , . . . , αnj 11 q j 1
¸
n 1
aj ~gj
j 1
q est génératrice de G.
4. (a) De même qu’au 2. :
1q 0R
n 1
ņ
ô
ai α1i , . . . ,
i 0
j 1
ņ
ai αni
0R
n 1
1
i 0
En réindiçant avec i j 1 on obtient :
¸
n 1
aj ~gj
0R
n 1
ô pApα1q, . . . , Apαn 1qq 0R
n 1
j 1
Finalement
¸
n 1
aj ~gj
0R
n 1
ô Apα 1 q . . . Apα n 1 q 0
j 1
(b) A est un polynôme de degré n et admet n 1 racines distinctes qui sont les αi (1 ¤ i ¤ n 1).
Nécessairement A est le polynôme nul et par conséquent tous ses coefficients aj sont nuls.
Donc la famille p~g1 , . . . , ~gn
5.
1
q est libre.
G contient une famille libre (4.) et génératrice (3.), donc une base à n
G étant un s.e.v. de Rn
1
de même dimension que Rn
6. Posons pβ1 , . . . , βn 1 q un vecteur quelconque de Rn
il existe un polynôme L P Rn rX s tel que @i P rr1, n
1
1
1 éléments soit dim G n
on a donc G Rn
comme G Rn
1ss, Lpαi q βi .
1
1
.
alors :
Reste à prouver l’unicité de ce polynôme L.
Supposons L1 et L2 deux polynômes de Rn 1 tels que @i P rr1, n 1ss, L1 pαi q L2 pαi q βi .
Remarquons alors que @i P rr1, n 1ss, L1 pαi q L2 pαi q 0 donc tous les αi sont racines du polynôme
L1 L2 . Celui-ci étant de degré inférieur ou égal à n et ayant alors n 1 racines distinctes ont en
déduit qu’il s’agit du polynôme nul, d’où l’unicité !
Le théorème de Lagrange précédemment cité est donc bien prouvé.
Lycée de l’Essouriau - Les Ulis
3
PCSI
1.