PGCD : D`Euclide à Bézout

Chapitre III
PGCD : D’Euclide à Bézout
1
PGCD de deux entiers
☞ Activités 1 et 2 page 34 pour se rafraîchir la mémoire et découvrir quelques propriétés
du PGCD.
Considérons un entier relatif a. On notera D(a) l’ensemble de ses diviseurs dans Z.
Par exemple, D(0) = Z, D(1) = {−1; 1},D(12) = {−12; −6; −4; −3; −2; −1; 1; 2; 3; 4; 6; 12}.
Pour tout a ∈ Z, 1 ∈ D(a). D(a) est donc non vide. De plus, |a| est le plus grand élément de
D(a). D(a) est donc majoré.
Définition 1 :
Soit a et b deux entiers non simultanément nuls. On appelle PGCD de a et b et on note
P GCD(a; b) ou a ∧ b le plus grand entier naturel qui divise simultanément a et b.
Le PGCD de a et b est donc le plus grand élément de D(a) ∩ D(b). Comme toute partie
non vide et majorée de N admet un plus grand élément, cette définition en est bien une car
D(a) ∩ D(b) contient au moins 1.
Exemple 1 :
1. Écrire la liste des diviseurs de 30 et de −30 puis de 12 et de −12.
2. En déduire que P GCD(30; 12) = P GCD(30; −12) = P GCD(−30; 12) = P GCD(−30; −12) =
6.
Remarque 1 Pour tous a, b ∈ Z, on a P GCD(a, b) = P GCD(−a, b) = P GCD(a, −b) =
P GCD(−a, −b). On travaillera donc désormais avec des entiers naturels.
Propriété 1 : Pour tous a, b ∈ N non simultanément nuls :
• P GCD(a; b) = P GCD(b; a)
• P GCD(a; a) = a
• P GCD(a; 0) = a
• P GCD(a; 1) = 1
• b|a si et seulement si P GCD(a; b) = b
• Pour tout k ∈ N, P GCD(ka; kb) = k × P GCD(a; b)
Démonstration : en classe
Définition 2 On dit que deux entiers naturels sont premiers entre eux si leur PGCD est 1.
1
2
Algorithme d’Euclide
Euclide a vécu au 3ème siècle avant notre ère en Grèce. Il est considéré comme le "père
de la géométrie". Son ouvrage le plus célèbre, les Éléments, comprenant 13 tomes est un
des plus anciens traités connus présentant de manière systématique, à partir d’axiomes et
de postulats et avec des démonstrations, un large ensemble de théorèmes sur la géométrie
et l’arithmétique. Ce traité est, paraît-il, le livre qui s’est le plus vendu au monde après la
bible.
Lemme 1 (d’Euclide) Soit a et b deux entiers naturels non nuls et r le reste dans la
division euclidienne de a par b. Alors P GCD(a; b) = P GCD(b; r)
Idée de la démonstration : De l’égalité a = bq + r, on tire que D(a; b) = D(b; r)
Algorithme 1 (d’Euclide) :
Soit a et b deux entiers naturels non nuls. La suite des divisions euclidiennes suivantes finit
par s’arrêter :
de a par b : a = bq0 + r0 , avec 0 ≤ r0 < b
de b par r0 : b = r0 q1 + r1 avec 0 ≤ r1 < r0
de r0 par r1 : r0 = r1 q2 + r2 avec 0 ≤ r2 < r1
.
.
.
de rn−2 par rn−1 : rn−2 = rn−1 qn + rn
de rn−1 par rn : rn−1 = rn qn+1 + 0
On a alors : P GCD(a; b) = rn , dernier reste non nul.
Idée de démonstration : La suite (rn ) est strictement décroissante et à valeurs dans N donc
il existe n0 ∈ N tel que rn0 = 0. Le reste découle du lemme précédent.
Exemple 2 Calculer P GCD(585; 481) :
585 = 481 × 1 + 104
481 = 104 × 4 + 65
104 = 65 × 1 + 39
65 = 39 × 1 + 26
39 = 26 × 1 + 13
26 = 13 × 2 + 0
Donc P GCD(585; 481) = 13.
Remarque 2 :
– Cet algorithme, vieux de plus de 2 millénaires, est assez performant. Il a
fallu attendre la fin du 18ème siècle pour qu’un mathématicien français,
Gabriel Lamé démontre, en utilisant la suite de Fibonacci et le nombre
d’or, que cet algorithme trouve le PGCD des entiers a et b en moins de
5k étapes, où k est le nombre de chiffres décimaux de b.
2
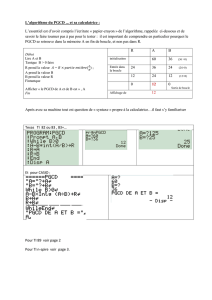
– Voici l’algorithme d’Euclide en langage Casio (bien qu’il existe une fonction donnant
directement le PGCD de deux entiers) :
"a" : ? -> a
"b" : ? -> b
While b!=0
a-b*Int(a/b)-> r
b -> a
r -> b;
WhileEnd
"PGCD(a,b)=" a
3
Théorème de Bézout
Étienne Bézout, mathématicien français né en 1730, a établi que
le PGCD de deux entiers est en fait une combinaison linéaire de
ces deux entiers. Ce résultat avait déjà été démontré au début du
17ème siècle par Bachet de Méziriac mais Bézout l’a généralisé et
a laissé son nom à la postérité.
3.1
Égalité de Bézout
Théorème 1 Soit a et b deux entiers relatifs.
Si d = P GCD(a; b), alors il existe deux entiers u et v tels que
au + bv = d
Démonstration (du site de G.Connan) :
Considérons d’abord le cas où a et b sont non nuls et notons
S = {au + bv; u ∈ Z, v ∈ Z et au + bv > 0}
L’ensemble S est constitué d’entiers naturels et est non vide car il contient au moins a2 +b2 : il
admet donc un unique plus petit élément que nous noterons d qui s’écrit donc d = au0 +bv0 .
Notre mission va bien sûr consister à prouver que d est en fait le PGCD de a et b.
Nous allons pour cela utiliser une ficelle classique : introduire le reste de la division euclidienne de a par d et utiliser le fait que d est le plus petit élément de S puis raisonner par
l’absurde.
La division de a par d s’écrit
a = dq + r
avec 0 ≤ r < d
Supposons que r > 0, alors
r = a − dq = a − q(au0 + bv0 ) = a(1 − qu0) + b(−qv0 ) > 0
3
et donc r ∈ S or r < d. C’est impossible car d est le plus petit élément de S : contradiction.
Notre supposition de départ est donc fausse et r = 0. Nous en déduisons que d divise a.
On montre de manière similaire que d divise b. Ainsi
d est un diviseur commun de a et b
Il nous reste à montrer que c’est le plus grand. Soit δ un diviseur commun à a et b
quelconque. On a montré au début du cours qu’alors δ divisait toute combinaison linéaire de
a et de b, donc en particulier δ divise au0 + bv0 donc d. Alors toujours δ ≤ |d| = d, donc d est
bien le plus grand des diviseurs.
Il faut encore vérifier que le PGCD est unique. La méthode habituelle est de supposer
qu’il existe un deuxième PGCD, disons d′ . Alors d ≤ d′ car d′ est le plus grand diviseur puis
d′ ≤ d car d aussi et finalement d = d′ ce qui assure l’unicité.
Comme |a| = ±1 × a + 0 × 0, l’égalité tient toujours si b est nul. Il en est de même si a
est nul.
3.2
Théorème de Bézout
Théorème 2 Soit a et b deux entiers relatifs.
a et b sont premiers entre eux si et seulement si il existe deux entiers u et v tels que
au + bv = 1.
Démonstration :
Le sens direct découle du théorème précédent.
Pour la réciproque, l’égalité au + bv = 1 entraîne que le PGCD de a et b divise 1...
3.3
Algorithme d’Euclide étendu
Cet algorithme retourne le PGCD d de deux entiers a et b ainsi que les coefficients de
Bézout u et v tels que au + bv = d.
Voir activité 46 page 49.
À partir de la suite (rn ) des restes des divisions euclidiennes
de l’algorithme d’Euclide, on construit deux suites (un ) et
(vn ) telles que, pour tout n, rn = aun + bvn .
Initialisation : r0 = a ; r1 = b ; u0 = 1 ; u1 = 0 ; v0 = 1 ;
v1 = 1.
On a alors r0 = au0 + bv0 et r1 = au1 + bv1 .
Relation de récurrence : Si rn = rn+1 × qn+1 + rn+2 est la
division de l’algorithme d’Euclide à l’étape n + 1, on a :
rn+2 = aun+2 + bvn+2 avec un+2 = un − un+1 × qn+1 et
vn+2 = vn − vn+1 × qn+1 . Il s’agit donc d’une relation de
récurrence d’ordre 2.
Sortie : Soit N tel que rN +2 = 0. On a alors rN +1 =
P GCD(a; b) = auN +1 + bvN +1
4
En langage Casio :
4
Théorème de Gauss
Surnommé le Prince des mathématiciens, Carl Friedrich Gauss
(1777-1855) étudia tous les domaines des mathématiques et contribua à développer la plupart des branches des sciences.
Théorème 3 Soit a, b et c trois entiers non nuls.
Si a|bc et si b et c sont premiers entre eux alors a|c.
Démonstration :
Il existe k tel que bc = ka.
D’après Bézout, il existe u et v tels que au+bv = 1 soit cau+cbv = c c’est-à-dire acu+akv = c.
Donc a|c.
Corollaire 1 Soit a, b, c trois entiers non nuls.
Si a et b divisent c et a et b sont premiers entre eux, alors ab divise c.
5
5
5.1
Quelques applications
Équations diophantiennes
6
5.2
Chiffrement affine
7