C.G

Atelier de Maths : Récurrence
Introduction Comment démontrer : Si on retire une case quelconque d’un
échiquier 2n × 2n on peut paver la partie restante à l’aide de pièces de trois
cases en forme de L
Vérifions les premiers cas
Le cas n = 1 est facile à vérifier, on peut aussi vérifier le cas n = 2 et ensuite ?
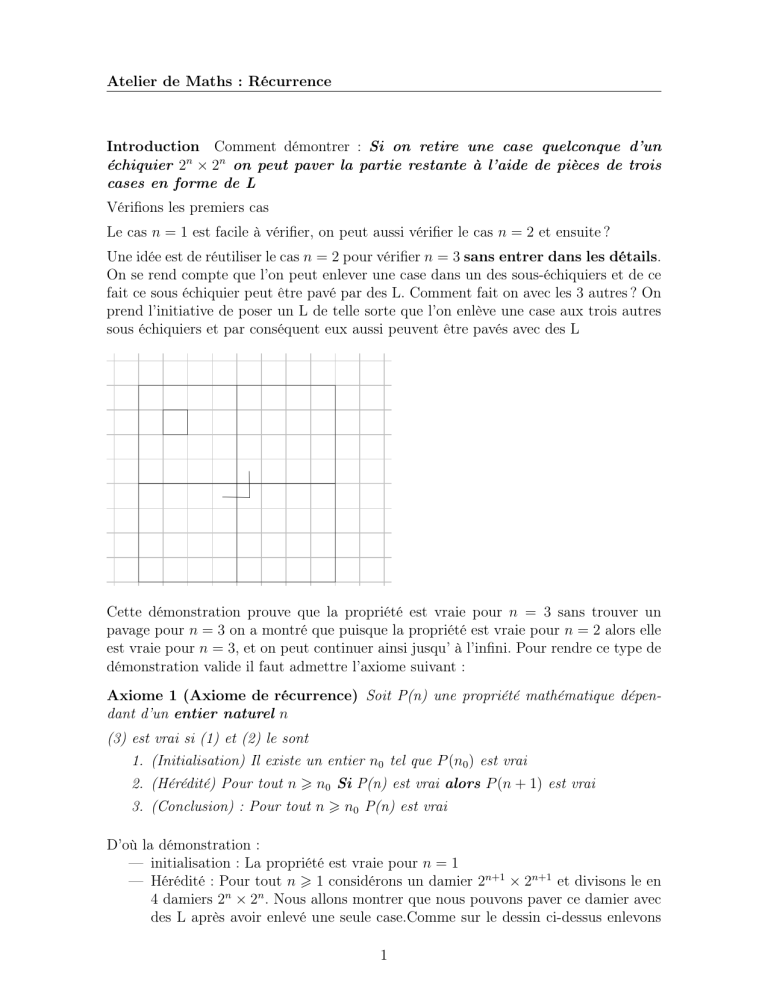
Une idée est de réutiliser le cas n = 2 pour vérifier n = 3 sans entrer dans les détails.
On se rend compte que l’on peut enlever une case dans un des sous-échiquiers et de ce
fait ce sous échiquier peut être pavé par des L. Comment fait on avec les 3 autres ? On
prend l’initiative de poser un L de telle sorte que l’on enlève une case aux trois autres
sous échiquiers et par conséquent eux aussi peuvent être pavés avec des L
Cette démonstration prouve que la propriété est vraie pour n = 3 sans trouver un
pavage pour n = 3 on a montré que puisque la propriété est vraie pour n = 2 alors elle
est vraie pour n = 3, et on peut continuer ainsi jusqu’ à l’infini. Pour rendre ce type de
démonstration valide il faut admettre l’axiome suivant :
Axiome 1 (Axiome de récurrence) Soit P(n) une propriété mathématique dépendant d’un entier naturel n
(3) est vrai si (1) et (2) le sont
1. (Initialisation) Il existe un entier n0 tel que P (n0 ) est vrai
2. (Hérédité) Pour tout n > n0 Si P(n) est vrai alors P (n + 1) est vrai
3. (Conclusion) : Pour tout n > n0 P(n) est vrai
D’où la démonstration :
— initialisation : La propriété est vraie pour n = 1
— Hérédité : Pour tout n > 1 considérons un damier 2n+1 × 2n+1 et divisons le en
4 damiers 2n × 2n . Nous allons montrer que nous pouvons paver ce damier avec
des L après avoir enlevé une seule case.Comme sur le dessin ci-dessus enlevons
1
une case dans 3 damiers de telle sorte qu’on ait enlevé un L on peut considérer
que l’on a pavé les 3 damiers avec des L en appliquant l’hypothèse de récurrence
et la seule case que l’on peut enlever on l’utilise pour le quatrième damier ce
qui nous permet d’appliquer encore une fois l’hypothèse de récurrence et ainsi le
pavage est terminé
— Conclusion : D’après l’axiome de récurrence la propriété est vraie pour tout n > 1
Problèmes
1. Un L-triomino de taille d’ordre n est la juxtaposition en forme de L de 3 damiers
carrés contenant 2n × 2n petits carrés . Montrer que tout L-triomino peut être
pavé par des pièces de trois cases en forme de L .
2. Démontrer que pour tout n , 22n − 1 est divisible par 3
3. En Sikinie, toutes les routes sont à sens unique.Deux villes quelconques sont
connectées par xectement une route directe.Montrer qu’il existe une ville qui
peut être rejointe à partir de n’importe quelle autre soit directement soit en
passant par une seule ville intermédiaire
4. Démontrer pour tout n > 2 :
v s
u
r q
u
√
t
2 3 4... (n − 1) n < 3
5. Étudier la convergence de la suite (un ) définie par son premier terme u0 , réel
1
√
positif, et la relation de récurrence : ∀n ∈ N, un+1 = un +
n+1
6. (CG 2014 : Problème 1 Question 1) Soit (xn ) une suite de réels telle que :
(a) x0 > 0
(b) Il existe deux réels et q strictement positifs tel que pour tout n > 0 on a
0 6 xn+1 − qxn 6 On pose bn = xn+1 − qxn
Montrer que pour tout n > 1 on a xn = q n x0 + q n−1 b0 + q n−2 b1 + ... + bn−1
7. (CG 2011 : Exercice 2) Un acheteur a dans son porte-monnaie n pièces. Notons
a1 , ..., an la valeur faciale de ces pièces , ce sont des nombres entiers strictement
positifs. Convenons d’ appeler capacité de ce porte monnaie le plus grand nombre
entier M tel que l’ on puisse payer sans rendu de monnaie toute somme (entière)
de 1 à M . Notons C(a1 , ..., an ) la capacité du porte monnaie contenant les pièces
a1 , ..., an .
On suppose que l’on a a1 = 1 et a1 6 a2 6 ... 6 an
(a) Calculer les capacités C(1,2,4),C(1,2,5) et C(1,2,3,4,5).
(b) Soit j un nombre entier compris entre 1 et n−1 et fixons les nombres a1 , ..., aj .
À quelle condition sur aj+1 a-t-on C(a1 , ..., aj ) = C(a1 , ..., aj , aj+1 ) ?
(c) Donner une méthode pour calculer C(a1 , ..., an )
(d) On fixe n. Comment choisir les nombres entiers a1 , ..., an pour que la capacité
C(a1 , ..., an ) soit la plus grande possible ?
2
Parfois on a besoin d’un axiome de récurrence légèrement différent que le précédent
Axiome 2 (Axiome de récurrence (fort)) Soit P(n) une propriété mathématique
dépendant d’un entier naturel n
(3) est vrai si (1) et (2) le sont
1. (Initialisation) Il existe un entier n0 tel que P (n0 ) est vrai
2. (Hérédité) Pour tout n > n0 Si P(k) est vrai pour tout les n0 6 k 6 n alors
P (n + 1) est vrai
3. (Conclusion) : Pour tout n > n0 P(n) est vrai
Résolvons avec l’axiome 2 l’exercice suivant :
La suite de Fibonnacci est définie par F0 = 0 et F1 = 1 avec Fn+2 = Fn+1 +Fn pour tout
n
φn − φ
n > 0. Démontrons par récurrence que tout terme de cette suite Fn vérifie Fn = √
5
√
√
1+ 5
1− 5
avec φ =
et φ =
2
2
1. On montre d’abord que φ et φ sont solutions de x2 − x − 1 = 0 donc pour tout
n
n−1
n−2
n > 2 on a φn = φn−1 + φn−2 et φ = φ
+φ
0
φ0 − φ
=0
2. Initialisation : vrai pour n = 0 car F0 = 0 d’une part et d’autre part √
5
1
φ1 − φ
d’où l’égalité . Vrai pour n = 1 car F1 = 1 et √
=1
5
n−1
3. Hérédité : Pour tout n > 2 on a Fn = Fn−1 + Fn−2
φn−1 − φ
√
=
5
n−2
φn−2 − φ
√
+
5
par hypothèse de récurrence
n−1
n−2
n
φn−1 + φn−2 − (φ
+φ )
φn − φ
√
√
Donc Fn =
=
d’après 1)
5
5
n
φn − φ
4. D’après l’axiome de récurrence Fn = √
pour tout n > 0
5
Problèmes
n
P
1.
Fi2 = Fn Fn+1
2.
3.
i=1
n
P
Fi = Fn+2 − 1
i=1
2n+1
P
i=1
impair
Fi = F2n+2 et
2n
P
Fi = F2n+1 − 1
i=2
pair
4. Fn−1 Fn+1 = Fn2 + (−1)n
5. Si m|n alors Fm |Fn
n−2 n−3
6. Fn = n−1
+ 1 + 2 +... =
0
P
k=1
n−k>k−1
n−k
k−1
puis la suite 0, 1, 2... tant que n − k > k − 1
3
On écrit la suite n−1, n−2, n−3...
Atelier de Maths : Les polynômes
Introduction Comment retrouver par le calcul qu’une famille de courbes ont un ou
plusieurs points fixes ? Par exemple sur le dessin ci-dessus il s’agit d’une famille de
paraboles d’équation y = a(x − 2)2 + 1 pour a ∈ [−5; 5] et il semble que toutes les
paraboles passent par le point de coordonnées (2 ; 1)
On associe à ces courbes une fonction fa (x) = a(x − 2)2 + 1 définie sur R avec a ∈ R
Définissons à présent le problème de la recherche de point fixe :
Existe -il un ou plusieurs points de coordonnées (x0 ; y0 ) tel que pour tout a ∈ R
fa (x0 ) = y0
Pour insister sur le rôle des quantificateurs on peut écrire :
∃?(x0 ; y0 )∀a ∈ Rfa (x0 ) = y0
Nous allons nous restreindre au cas où fa (x) est un polynôme en x mais aussi un
polynôme en a
√
x−1
et x + 1 ne sont
Par exemple un polynôme réel en x est 2x3 − 3x + 1 alors que 2
x +1
pas des polynômes
2y 3 −3y +1 est le même polynôme que 2x3 −3x+1 , ce qui compte ce sont les coefficients
1, -3 pour −3x ou −3y ,0 car il n’y a pas de termes en x2 et 2 pour 2y 3
k=n
P
Définition : P est un polynôme à coefficients réels si P =
ak xk où les ak sont des
k=0
nombres réels. On peut identifier P à la suite de nombres réels (a0 , a1 , ..., an ) nulle à
partir d’un certain rang
4
Le degré de P est le plus grand indice n des coefficients non nuls de P . on note d(P )
Division euclidienne de polynômes et racines d’un polynômes Théorème et
Définition :Etant donnés deux polynômes A et B , il existe deux polynômes Q et R
uniques tel que
A = BQ + R
avec d(R) < d(B)
Q est le quotient et R le reste de la division de A par B
Si R = 0 on dit que B divise A que l’on note B|A
Par exemple X 3 + 1 = (X − 1)(X 2 + X + 1) + 2
On peut poser la division ainsi :
X3 + 1
−(X 3 − X 2 )
X2 + 1
−(X 2 − X)
X +1
−(X − 1)
2
X −1
X +X +1
2
Définition : α ∈ R et P =
k=n
P
ak xk , on note P (α) =
k=0
k=n
P
ak α k
k=0
On dit α est racine de P lorsque P (α) = 0
Propriété : α racine de P ⇐⇒ X − a|P
Définition : Le polynôme nul est le polynôme dont tous les coefficients sont nuls
Propriété : Si pour tout a ∈ I où I est un intervalle de R on a P (a) = 0 si et seulement
si P = 0
Application : ∃?(x0 ; y0 )∀a ∈ Rfa (x0 ) = a(x0 − 1)2 + 1 = y0
⇐⇒ a(x0 − 1)2 + 1 − y0 = 0 pour tout a ∈ R
On regarde l’expression a(x0 − 1)2 + 1 − y0 comme un polynôme en a , on applique la
propriété ci-dessus donc les coefficients (x0 − 1)2 et 1 − y0 sont nuls donc x0 = 1 et
y0 = 1
A vous de jouer Ici fa (x) = a(x2 − 1) − 1 (voir dessin plus bas)
Relation racines et coefficients : Si le polynôme x2 + px + q = (x − x1 )(x − x2 )
en développant et en identifiant on a p = −(x1 + x2 ) et q = x1 x2
Si le polynôme x3 + px2 + qx + r = (x − x1 )(x − x2 )(x − x3 ) en développant et en
identifiant on a p = −(x1 + x2 + x3 ) ,q = x1 x2 + x2 x3 + x1 x3 et r = −x1 x2 x3
Exercice : Soit x1 , x2 et x3 les racines du polynôme x3 +3x2 −7x+1. Calculer x21 +x22 +x23
5
Polynômes réciproques Le polynôme P = (a0 , a1 , ..., an ) est dit réciproque si an−i =
ai pour i variant de 0 à n
Exemples : y 5 + 1, x3 + 3x2 + 3x + 1
1
Théorème : Tout polynôme réciproque P de degré pair 2n vérifie :P (x) = xn Q(x+ )
x
1
1
Exemple : x4 + 4x3 + 6x2 + 4x + 1 = x2 ((x + )2 + 4(x + ) + 4)
x
x
Polynômes symétriques et symétriques élémentaires P (x, y) est symétrique si
P (x, y) = P (y, x)
Exemples : P (x, y) = 2x2 + 4xy + 2y 2 = P (y, x)
Les polynômes symétriques élémentaires sont : σ1 = x + y, σ2 = xy et les si = xi + y i
avec i = 0, 1, ...n
Théorème : s0 = 2, s1 = σ1 et sn = σ1 sn−1 − σ2 sn−2 pour n > 2
Par exemple s2 = σ12 − 2σ2
Théorème : Tout polynôme symétrique élémentaire est un polynôme en σ1 et en σ2
Exemple : 2x2 + 4xy + 2y 2 = 2(x2 + y 2 ) + 4xy = 2(x + y)2 − 4xy + 4xy = 2σ12
Problèmes
1. m|n ⇐⇒ xm − am |xn − an
2. Factoriser sur Z , x10 + x5 + 1
3. Montrer que 1 + x + x2 + x3 + x4 | 1 + x11 + x22 + x33 + x44
k=n
k=n
P
P
4. Si P =
ak xk alors on définit son polynôme dérivé par P 0 =
kak xk−1
k=0
k=1
Montrer que pour tout x on a P (x) = P (a) + (x − a)P 0 (a)
6
5. Déterminer un polynôme à coefficients entiers admettant comme racine :
√
√
(a) 2 + 3
√
√
(b) 2 + 3 3
6. Soient x1 et x2 les racines de x2 + px + q et x01 et x02 les racines de x2 + p0 x + q 0 .
Exprimer en fonction de p, p0 , q, q 0 :
(a) (x1 − x01 )(x2 − x01 )(x1 − x02 )(x2 − x02 )
(b) (x1 − x01 )(x2 − x01 )(x1 + x02 )(x2 + x02 )
7. Pour quelles valeurs de a les polynômes x2 + ax + 1 et x2 + x + a ont une racine
commune ?
8. Prouver que pour tout entier naturel x2 + x + 1|(x + 1)2n+1 + xn+2
9. f (n) = n2 − n + 41 donne des nombres premiers pour tout entier n entre 1
et 40. Trouver 40 valeurs consécutives de n pour lesquelles f (n) est composé.
Généraliser
10. Montrer que (1+x+...+xn )2 −xn est le produit de deux polynômes à coefficients
entiers
11. (CG 2007 Ex 1) On appelle fonctions de type T0 les fonctions « trinômes » sur
[-1, 1], définies par : t : [−1, 1] → R , x → t(x) = ax2 + bx + c
a, b, c étant des réels quelconques. Pour tout entier naturel non nul n, on appelle
fonctions de type Tn les fonctions de la forme f +λ|g|, λ étant un réel quelconque
et f, g des fonctions quelconques de type Tn−1 .
(a) Établir que la fonction φ définie par φ(x) = 0 pour tout x de [-1,0] et φ(x) = x
pour tout x de [0, 1], est de type T1
(b) On considère deux fonctions trinômes t1 et t2 telles que t1 (0) = t2 (0) et on
définit la fonction f : [−1, 1] → R telle que :
Pour tout réel x de [-1,0], f (x) = t1 (x) et pour tout réel x de [0,1], f (x) =
t2 (x). Démontrer qu’ il existe un entier naturel N tel que la fonction f soit
de type TN .
7
Atelier de Maths : géométrie plane vectorielle
Vecteurs
Dictionnaire
−→
−→
1. A, B, C alignés ⇐⇒ il existe k ∈ R tel que AB = k AC
−→ −−→
2. Les droites (AB) et (CD) sont parallèles ⇐⇒ AB et CD sont colinéaires.
−→ −−→
3. Les droites (AB) et (CD) sont perpendiculaires ⇐⇒ AB.CD = 0.
Barycentres On s’intéresse au problème suivant :
Sur une tige (dont on néglige la masse) on place deux points A et B. en ces points on
place une masse α pour le Point A et β pour le point B (avec α + β 6= 0).
On veut placer le point G tel que la tige sera en "équilibre" si on la suspend ce point.
On appelle ce point G barycentre des points (A, α) et (B; β)
Un premier cas : α = β(6= 0) (on parle d’isobarycentre)
−→ −−→ →
−→
−−→ →
−
−
Le point G est le milieu du segment [AB] ⇔ GA + GB = 0 ⇔ αGA + β GB = 0
Cas général pour deux points : soit α et β deux réels tels que α + β 6= 0
−→
−−→ →
−
G = bar((A, α); (B, β)) ⇔ αGA + β GB = 0
−−→
−−→
−−→
⇔ pour tout point M αM A + β M B = (α + β)M G
Caractérisation :
— C ∈ (AB) ⇐⇒ ∃(α; β) ∈ R2 tels que C = bar((A, α); (B, β))
— C ∈ [AB] ⇐⇒ ∃(α; β) ∈ (R+ )2 tels que C = bar((A, α); (B, β))
Cas général pour n points
Soit (α1 , α2 , ..., αn ) ∈ Rn tel que
n
X
αi 6= 0 et A1 , ...An n points
i=1
G = bar((A1 , α1 ); ...; (An , αn )) ⇔
n
X
−−→ →
−
αi GAi = 0
i=1
⇔ pour tout point M ,
n
X
n
−−→ X −−→
αi M A i =
αi M G
i=1
i=1
Associativité du barycentre
caractérisation :
— points coplanaires
— intérieur du triangle ABC
— régionnement du plan
8
Problèmes
1. Relation et droite d’Euler
Soit un triangle ABC, G le centre de gravité du triangle, O le centre du cercle
qui lui est circonscrit et H le point défini par :
−→ −→ −→ −→
OH = OA + OB + OC
(1)
−→ −→ −→ −→ −→ −→
(a) Montrer que AH.BC = BH.CA = CH.AB = 0
Que peut-on en déduire pour le point H ?
−→
−→
(b) Déduire de l’égalité (1) que OH = 3OG (relation d’Euler).
Que peut-t-on en déduire sur les trois point O,G et H ?
2. Parallélogramme de Varignon : Montrer que dans un quadrilatère, les milieux
des côtés sont les sommets d’un parallélogramme.
3. (a) Soit A,B,C et D quatre points . Montrer que :
−→ −→ −→ −→ −→ −→
DA.BC + DB.CA + DC.AB = 0
(b) Application : Retrouver que les hauteurs d’un triangle sont concourantes.
4. Soit ABC un triangle : on utilisera les notations suivantes : AB=c, AC=b et
BC=a O désigne le centre du cercle circonscrit au triangle ABC, H son orthocentre et G son centre de gravité.
(a) Prouver que
a cos A + b cos B + c cos C = 2(a cos B cos C + b cos C cos A + c cos A cos B) =
2c sin A sin B
−→
−→ −→ −→
(b) À l’aide de la relation d’Euler OH = OA + OB + OC, montrer que O est
barycentre du système
{(A, a cos A), (B, b cos B), (C, c cos C)}
(c) Prouver que l’on a aussi
O = bar{(A, sin 2A), (B, sin 2B), (C, sin 2C)}
5. Soit ABC un triangle non plat et une droite ∆ qui coupe respectivement (BC),(CA)
et (AB) en P,Q,R distincts des sommets.
(a) Utiliser la parallèle à ∆ en B pour établir la relation de Ménélauss :
PB QC RA
.
.
=1
PC QA RB
(b) Démontrer la réciproque
(c) En déduire le théorème de Ceva : Si ABC est un triangle non plat et si P,Q,S
sont des points respectivement situés sur (BC),5CA),(AB), en dehors des
sommets, alors les droites (AP),(BQ) et (CR)sont concourantes ou parallèles
si et seulement si on a :
PB QC RA
.
.
= −1(relation de Ceva)
PC QA RB
9
6. Dans un triangle ABC isocèle en A, on note A’ le milieu de [BC], H le projeté
orthogonal de A’ sur (AC), I le milieu de [A’H]. Montrer que (AI) est orthogonale
à (BH).
−→
−→
−
−
7. Rappel : Soit →
u et →
v deux vecteurs unitaires et de même sens que AB et AC,
−
−
alors la droite passant par A et dirigée par →
u +→
v est la bissectrice intérieure
issue de A dans le triangle ABC.
Soit ABC un triangle : on utilisera les notations suivantes : AB=c, AC=b et
BC=a
Soit I le barycentre du système {(A, a), (B, b), (C, c)}
Montrer que I appartient à chaque bissectrice intérieure du triangle ABC c’est
à dire que I est le centre du cercle inscrit du triangle ABC.
−
−
−
−
−
−
8. Soit →
u ,→
v ,→
w trois vecteurs du plan. Montrer que →
w =→
u +→
v équivaut à :
−
−
−
−
−
−
−
−
−
k→
w k2 − k→
w −→
u k2 − k→
w −→
v k2 = k→
u k2 + k→
v k2 − k→
u −→
v k2
9. Soit ABC un triangle non plat dont les côtés [BC],[CA] et [AB]ont pour longueurs
respectives a , b et c. Montrer que les deux médianes[BB’] et [CC’]issues de B et
de C sont orthogonales si et seulement si b2 + c2 = 5a2
10. Démontrer que dans un trapèze les milieux des côtés parallèles , ainsi que le point
de concours des diagonales et le point de concours des droites non parallèles sont
alignés
11. Problème de construction : Deux droites sont sécantes à l’extérieur d’une feuille.
Construire la droite passant par A et le point d’intersection des 2 droites en ne
faisant des tracés géométriques qu’à l’intérieur de la feuille
12. (CG 2005) On considère dans le plan trois points A0 , B, C non alignés. On
désigne par A1 le centre du cercle inscrit dans le triangle A0 BC . On poursuit le
processus en considérant A2 , le centre du cercle inscrit dans le triangle A1 BC,
etc. Ainsi, pour tout i entier naturel, Ai+1 est le centre du cercle inscrit dans le
triangle Ai BC.
Démontrer qu’ il existe un point A, limite de la suite (An ), c’est-a-dire tel que
AAn tende vers 0 et préciser sa position.
Que devient le résultat précédent si, a chaque étape, pour i = 0 ,1,2,..., on prend
pour Ai+1 l’ orthocentre du triangle Ai BC au lieu du centre du cercle inscrit ?
10
Atelier de Maths : Dénombrement
Arrangement de p éléments parmi n où 0 6 p 6 n 10 chevaux numérotés de 1
à 10 sont au départ d’une course. Combien de tiercés (dans l’ordre) possible ?
Un tiercé est un triplet (x1 , x2 , x3 ) où chaque xi est un entier entre 1 et 10 et les xi sont
différents deux à deux. Il y a 10 possibilités pour le premier , puis 9 pour le second et
8 pour le troisième. Donc il y a 10 × 9 × 8 = 720 tiercés possibles
En étiquetant les objets que l’on dénombre par des entiers on peut définir la notion
d’arrangement de la manière suivante :
Définition : Soit E = {1, 2, ..., n}. Un arrangement de p éléments parmi les n éléments
de E est un p-uplet (x1 , ..., xp ) où xi ∈ E
Théorème : Il y a n × (n − 1) × ... × (n − p + 1) arrangements de p éléments parmi n
Définition :Une permutation de n éléments est un arrangement de n éléments parmi
n
Théorème : Il y a n × (n − 1) × ... × 2 × 1 = n! permutations de n éléments
Combinaison de p éléments parmi n où 0 6 p 6 n 10 chevaux numérotés de 1 à
10 sont au départ d’une course. Combien de tiercés (dans le désordre) possible ?
Un tiercé dans le désordre est une partie de 3 éléments {x1 , x2 , x3 } de l’ensemble
{1, 2, ..., 10}
Chaque partie {x1 , x2 , x3 } peut engendrer 3! arrangements en faisant des permutations,
et de ce fait on retrouve les 10 × 9 × 8 = 720 tiercés possibles, donc le nombre de tiercés
10 × 9 × 8
= 120
dans le désordre est
3!
Définition : Une combinaison de p éléments parmi n éléments de E = {1, 2, ..., n} est
une partie de p éléments de E
n × (n − 1) × ... × (n − p + 1)
n!
Théorème : Il y a
= np = (n−p)!p!
combinaison de p
p!
éléments parmi n
Au Loto gagner au premier rang c’est trouver la combinaison de 5 nombres
parmi les 49
49
entiers de 1 à 49 plus le "numéro de chance" entre 1 et 10. Il y a 5 × 10 = 19068840
possibilités
Théorème :
n
1. np = n−p
n(n − 1)
2. n0 = 1, n1 = n, n2 =
2
n n−1
n
3. p = p p−1
n−1
4. np = n−1
+
p−1
p
n
P
n
5.
= 2n
k
k=0
11
Problèmes
1. Montrer que le nombre de diagonales d’un polygone convexe est égal au nombre
de paires de sommets auquel on retranche le nombre de côtés
2. Soit A les 26 lettres de l’alphabet de la langue française.
(xn ) une suite finie d’éléments de A avec n > 1 le nombre de lettres. Un mot m
définie à partir de (xn ) est x1 ...xn . Un anagramme de m est le mot obtenu en
faisant une permutation sur les lettres xi , par exemple ENA est un anagramme
de ANE (un anagramme n’a pas forcément de sens)
(a) En supposant que les lettres sont différentes entre elles, combien y-a-t-il
d’anagrammes ?Combien d’anagrammes pour le mot NOE ?
(b) Même question si on suppose que k lettres parmi les n sont identiques. Combien d’anagrammes pour le mot GRAMME ?
(c) Même question si on suppose l’existence de deux groupes identiques. Combien
d’anagrammes pour le mot ANAGRAMME ?
n
P
n 2
3. Prouver que
= 2n
k
n
k=0
4. Dans un jeu de 32 cartes, il y a 8 hauteurs : 7, 8, 9 , 10, Valet, Dame , Roi et
As et 4 couleurs : Coeur, Carreau, Pique et Trèfle. (Coeur et Carreau sont de
couleur rouge , Pique et Trèfle sont de couleur noire).
Dans un jeu de 52 cartes on rajoute les hauteurs 2,3,4,5 et 6.
Pour simplifier on dira qu’ une main au poker est une combinaison de 5 éléments
d’un jeu de cartes.
(a) Combien y-a-t-il de mains dans un jeu de 32 cartes ? dans un jeu de 52 cartes ?
(b) Une main contient un carré quand elle contient quatre cartes de même hauteur. Combien de mains contiennent un carré dans un jeu de 32 cartes ? (52
cartes)
(c) Une main contient un brelan quand elle contient trois cartes de même hauteur( mais pas quatre). Combien de mains contiennent un brelan dans un jeu
de 32 cartes ? (52 cartes)
(d) Une main contient une paire quand elle contient deux cartes de même hauteur( mais ni trois, ni quatre). Combien de mains contiennent une paire dans
un jeu de 32 cartes ? deux paires ?(52 cartes)
(e) Une main contient un full quand elle contient un brelan et une paire . Combien
de mains contiennent un full dans un jeu de 32 cartes (52 cartes)
5. Courses de chevaux (suite) : Combien y-a-t-il d’ordre d’arrivées possibles
pour une course de n chevaux en tenant compte des ex-aequo possibles. On
notera An le nombre d ’arrivées possibles.
(a) Que vaut A1 ? A2 ?
(b) Vérifier la relation de récurrence permettant de calculer An à partir de An−1 ,
n
P
n
An−2 , ...,A0 = 1 : An =
An−k
k
k=1
(c) Donner un algorithme permettant de calculer An
12
6. Nombre de régions dans un cercle
Avec 2 points sur un cercle en traçant 1 segment on délimite deux régions dans
le cercle, avec 3 points on délimite 4 régions , avec 4 points 8, avec 5 points 16,
on pourrait croire que le nombre de régions est égale à 2n−1 où n est le nombre
de points , ce qui est faux car pour n =
6 il y a 31 régions et non pas 32. Justifier
que le nombre de régions vaut n + n4 + n−1
2
7. Nombre de régions dans un cercle (suite) En supposant que le nombre
de régions est un polynôme P (n) avec n est le nombre de points
(a) Si P un polynôme de degré p on définit par récurrence :
∆1 (P )(n) = P (n + 1) − P (n) et ∆k (P ) = ∆1 (∆k−1 (P )) pour k > 2
Justifier que d◦ (∆1 (P )) = d◦ (P ) − 1 et en déduire que d◦ (∆p (P )) = 0 donc
∆p (P ) est une constante
(b) Application : On détermine les premières valeurs de P , 2,4,8,16,31 et 57, puis
on calcule les premières valeurs de ∆1 (P ), ∆2 (P ) et ∆3 (P ).
On observe que ∆4 (P ) = 1 sur les premières valeurs. En supposant que
∆4 (P ) = 1, donner un algorithme pour calculer P (n)
8. (CG 2012) :Un facteur doit distribuer le courrier dans une rue. Celle-ci ne comporte qu’une seule rangée de maisons régulièrement espacées et numérotées 1,
2, . . . , n, où n est un entier supérieur ou égal à 2. Le facteur doit distribuer
une lettre par maison. Pour cela, il laisse son vélo à la maison 1, y dépose le
courrier correspondant, et ensuite distribue les lettres au hasard, puis revient
à la maison 1 récupérer son vélo. Il effectue ainsi un trajet, représenté par les
numéros successifs des maisons où il a déposé le courrier. Par exemple, si n =
5, un trajet possible est 1, 5, 2, 4, 3, 1. La distance totale parcourue, appelée
longueur du trajet, vaut 12 dans ce cas car |5 - 1| + |2 - 5| + |4 - 2| + |3 - 4| +
|1 - 3| = 12. Un autre trajet possible est 1, 3, 5, 4, 2, 1, de longueur 8.
(a) Combien y a-t-il de trajets possibles ?
(b) Montrer que tout trajet est de longueur supérieure ou égale à 2(n - 1).
(c) Combien y-a-t-il de trajets de longueur minimale ?
13