Classe: 1S TP GeoGebra Travail à faire obligatoirement. Possibilité

Classe: 1S TP GeoGebra
Ce qui est affirmé sans preuve peut être nié sans preuve. Euclide d’Alexandrie
Travail à faire obligatoirement.
Possibilité de faire par binôme (binôme = 2 individus)
Vous pouvez envoyer vos travaux par e-lyco ou par e-mail ([email protected])
En cas de " panne ", n'hésitez pas à envoyer votre essai en décrivant précisément ce qui bloque.
Objectifs : apprendre à réfléchir … notamment à partir des équations, inéquations et les relations logiques (ET,
OU).
Ouvrir GeoGebra (version récente obligatoire).
Pour chaque partie I- II- III- créez un nouveau fichier.
I- Dans la ligne de saisie,
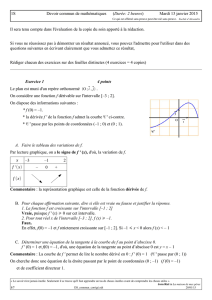
a) tapez : 2x + y – 5 < 0.
Qu'observez-vous ? (Décrivez précisément ce qui apparaît).
Le plan est partagé en deux demi-plans de frontière la droite d'équation 2x + y – 5 = 0.
La partie inférieure est colorée.
Copie d'écran :
« C'est à force d'observations, de réflexion que l'on trouve. Ainsi, piochons, piochons continuellement» Claude Monet
1/9 TP_GeoGebra-equation-inequation-logique-compte-rendu.odt 26/01/14

Classe: 1S TP GeoGebra
Ce qui est affirmé sans preuve peut être nié sans preuve. Euclide d’Alexandrie
Démontrez qu'un point M(x ; y) du plan appartient à la zone que vous avez observée à l'écran si et seulement si
y < –2x + 5
Soit un point de la frontière des deux demi-plans. Cette frontière est une droite .
L'ensemble des points N(x ; y) de cette droite  ont leurs coordonnées x et y qui sont solutions de l'équation :
y = –2x + 5.
Soit un point M(x ; y) de même abscisse x que N mais situé au-dessous de N :
on a donc :
yM
<
yN
, or,
yN
= –2x + 5.
Si M(x ; y) est en-dessous de  on a donc : y < –2x + 5 qui équivaut à 2x + y – 5 < 0.
Réciproquement :
Si y < –2x + 5, le point M de coordonnées (x ; y) est en-dessous du point N de coordonnées (x ; –2x + 5).
Or, quand x décrit ℝ, N décrit la droite  d'équation y = –2x + 5.
M et N ont la même abscisse.
le point M d'ordonnée quelconque apparaît si et seulement si son ordonnée est inférieure à celle de N qui est
égale à –2×(abscisse de N) + 5
Voir le fichier GeoGebra.
« C'est à force d'observations, de réflexion que l'on trouve. Ainsi, piochons, piochons continuellement» Claude Monet
2/9 TP_GeoGebra-equation-inequation-logique-compte-rendu.odt 26/01/14

Classe: 1S TP GeoGebra
Ce qui est affirmé sans preuve peut être nié sans preuve. Euclide d’Alexandrie
b) Qu'auriez-vous obtenu en remplaçant " < " par " > " ?
Qu'auriez-vous obtenu en remplaçant " < " par " = " ?
c) Vérifiez à l'aide du logiciel.
« C'est à force d'observations, de réflexion que l'on trouve. Ainsi, piochons, piochons continuellement» Claude Monet
3/9 TP_GeoGebra-equation-inequation-logique-compte-rendu.odt 26/01/14

Classe: 1S TP GeoGebra
Ce qui est affirmé sans preuve peut être nié sans preuve. Euclide d’Alexandrie
II- Dans la ligne de saisie,
a) tapez : (y>x+1) ∧ (y<–x+2)
(le symbole signifie "∧ ET ". Pour l'obtenir avec GeoGebra, cliquez
sur au bout de la ligne de saisie et choisissez le symbole)
qu'observez-vous à l'écran ? Expliquez.
b) a) tapez : (y>x+1) ∨ (y<–x+2)
(le symbole signifie "∨ OU ". Pour l'obtenir avec GeoGebra, cliquez
sur au bout de la ligne de saisie et choisissez le symbole)
qu'observez-vous à l'écran ? Expliquez.
Au a), la zone colorée est l'ensemble des points représentant les
solutions communes aux deux inéquations.
Au b), la zone colorée est l'ensemble des points représentant les solutions d'au moins une des deux inéquations.
Dans le premier cas, on obtient l'intersection (ET) de deux demi-plans,
l'un correspondant à l'inéquation : y > x + 1 ET l'autre à y < – x + 2.
Dans le second cas, on obtient la réunion (OU) des deux demi-plans. Tous les points dont les coordonnées
vérifient au moins une des deux inéquations sont colorées.
La partie non colorée correspond aux points dont les coordonnées ne vérifient aucune des deux équations.
« C'est à force d'observations, de réflexion que l'on trouve. Ainsi, piochons, piochons continuellement» Claude Monet
4/9 TP_GeoGebra-equation-inequation-logique-compte-rendu.odt 26/01/14

Classe: 1S TP GeoGebra
Ce qui est affirmé sans preuve peut être nié sans preuve. Euclide d’Alexandrie
« C'est à force d'observations, de réflexion que l'on trouve. Ainsi, piochons, piochons continuellement» Claude Monet
5/9 TP_GeoGebra-equation-inequation-logique-compte-rendu.odt 26/01/14