INITIATION PRATIQUE AU CALCUL INTÉGRAL Calcul d`aire

INITIATION PRATIQUE AU CALCUL INTÉGRAL
Calcul d’aire algébrique - Notion d’intégrale
Intégrale définie
L’intégrale d’une fonction f(x), ou f(t) selon la variable qui définit cette fonction,
définie entre deux bornes x
1 et x2 (ou t1 et t2
) de la variable, est égale à l’aire
algébrique (comptée positive si elle est au-dessus de l’axe de la variable, et
négative dans le cas contraire) de la surface délimitée par les 2 bornes x
1 et x2
entre l’axe d’une part et la courbe de la fonction f(x) d’autre part.
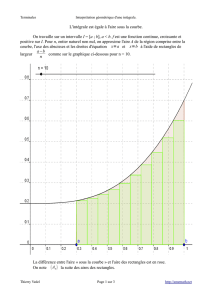
On remarque sur la figure 1 qu’en première approximation l’aire hachurée en
rouge peut se calculer par l’aire du trapèze:
A fx2fx1
2 . x2x1 f x1
moy
. x
l’approximation est d’autant plus fondée que l’écart x entre les 2 bornes x
1 et x2
sera faible; en zoomant encore davantage (x
2 x1
) on se rend compte alors que
f(x2) f(x1 ) et que l’aire A f(x1 ) . x
on va noter dx le petit accroissement x de la variable x à partir de la borne x
1;
dans ce cas la petite aire hachurée est quasiment celle du rectangle de base dx et de
hauteur f(x
1
) ;
on va noter dA l’aire de la petite surface ainsi obtenue;
si on veut maintenant calculer l’aire d’une grande surface entre 2 bornes éloignées,
on va décomposer l’intervalle en un grand nombre de petits trapèzes dont on va
calculer les aires en les approximant par des petits rectangles de largeur x dx
et de hauteur f(x
n), soit:
A f xn
x1
x3. x
que l’on notera:
A f xn
x1
x3 . dx
A s’appelle l’intégrale définie entre x
1 et x2
de la fonction f(x) et se lit:
Intégrale de x
1
à x 2 de f(x).dx ou encore
Somme de x
1
à x 2 de f(x).dx
application au calcul de l’aire de l’alternance positive de la sinusoïde ( figure1):
on calcule l’aire de chaque bandelette de largeur 1 carreau (6°) et de hauteur f(x
n)
soit A = f(xn) . 6°
on remarque qu’au-delà de 180°, A devient négatif et que le cumul décroit.
xn0 6 12 18 24 30 36
f(xn) 0 10 21 31 41 50 59
aire bandelette 0 60 126 186 246 300 354
aire cumulée 0 60 186 372 618 918 1272
xn42 48 54 60 66 72 78
f(xn) 67 74 81 87 91 95 98
aire bandelette 402 444 486 522 546 570 588
aire cumulée 1674 2118 2604 3126 3672 4242 4830
xn84 90 96 102 108 114 120
f(xn) 99 100 99 98 95 91 87
aire bandelette 594 600 594 588 570 546 522
aire cumulée 5424 6024 6618 7206 7776 8322 8844
xn126 132 138 144 150 156 162
f(xn) 81 74 67 59 50 41 31
aire bandelette 486 444 402 354 300 246 186
aire cumulée 9332 9776 10178 10532 10832 11078 11264
xn168 174 180 186 192 198 214
f(xn) 21 10 0 -10 -21 -31 -41
aire bandelette 126 60 0 -60 -126 -186 -246
aire cumulée 11390 11450 11450 11390 11264 11078 10832
l’aire totale de l’alternance positive vaut donc 11450 (valeur cumulée au point
x=180°); la valeur moyenne de l’alternance est égale à l’aire divisée par l’intervalle
choisi, soit 360°; la valeur moyenne vaut donc: 11450 / 180 = 63,6
on sait en électricité que la valeur moyenne d’une alternance se calcule par :
V moy = 2.V max / soit 2.100 / 3,1416 = 63,66
Intégrale indéfinie
L’intégrale indéfinie d’une fonction f(x) correspond au cas où les bornes x
1 et x2
ne sont pas spécifiées; dans le cas général on peut définir une fonction F(x)
appelée Intégrale indéfinie de f(x) ou encore Primitive de f(x) notée:
Fx f x . dx
Bernard PONTALIER INITIATION PRATIQUE AU CALCUL INTÉGRAL p.1/4

l’intégrale définie est alors égale à:
A f x
x1
x2 . dx F x2 F x1
Remarque : Les fonctions intégrales sont les fonctions inverses des fonctions
dérivées.
Bernard PONTALIER INITIATION PRATIQUE AU CALCUL INTÉGRAL p.2/4
-100
-80
-60
-40
-20
0
20
40
60
80
100
0 30 60 90 120 150 180 210 240 270 300 330 360
x1
x2
x3
figure 1

Ce calcul peut être automatisé au moyen d’une feuille de calcul Excel.
A B C D
1
2
3
4
x (°) f(x) f(x) . dx aire cumulée
0 0 0 0
=A2+6 =100*SIN(RADIANS(A3)) =B3*6 =D2+C3
=A3+6 =100*SIN(RADIANS(A4)) =B4*6 =D3+C4
Les courbes ci-dessous représentent l’évolution de la fonction f(x) en bleu et de
son intégrale (en mauve) calculée par l’aire cumulée à partir de l’origine (x = 0)
jusqu’à x = 360°
-120
-100
-80
-60
-40
-20
0
20
40
60
80
100
120
0 30 60 90 120 150 180 210 240 270 300 330 360
0
2000
4000
6000
8000
10000
12000
Les initiés reconnaitront aisément dans la courbe mauve la fonction (-cos x)
multipliée par un coefficient K qui ici est de l’ordre de 5750 et décalée d’une
quantité égale à la même valeur.
La variable x n’étant pas exprimée en radians comme le veut la mathématique,
mais en degrés, nous écrirons pour l’expression de la fonction y
1 = f(x):
y1 = f(x) = 100 sin 2 x
360
la courbe y
2
= F(x) représentant l’intégrale calculée de y
1
= f(x) s’écrira:
y2 = F(x) = - K cos 2 x
360 K
avec K = 5750 déduit de la courbe
Les mathématiques nous enseignent que la dérivée de la fonction y
2
s’écrit:
y '
2 =
F' (x) = - - K sin 2 x
360 . 2 360
y '
2 = 5750 . 2
360 sin 2 x 360 = 100,3 sin 2 x 360 y1 = f(x)
l’erreur commise par l’approximation que nous faisons lorsqu’on assimile l’aire
du trapèze à l’aire d’un rectangle est minime (ici 0,3%)
Quelques couples de fonctions Dérivées-Intégrale usuelles
intégration
fonction primitive
dérivation
dérivée fonction
f(x) = 0 F(x) = C (constante indéterminée)
f(x) = A (constante) F(x) = A.x + C
f(x) = a.x+b F(x) = a.x
2
/ 2 + b.x + C
f(x) = A.sin(x) F(x) = -A.cos(x) + C
f(x) = A.sin(b.x) F(x) = -(A/b) cos(b.x) + C
f(x) = A.cos(x) F(x) = A.sin(x) + C
f(x) = A.cos(b.x) F(x) = (A/b).sin(b.x) + C
f(x) = A.exF(x) = A.ex + C
f(x) = A.e
b.x
F(x) = (A/b).e
b.x
+ C
f(x) = A/x F(x) = A.Ln(x) + C
f(x) = A/b.x F(x) = (A/b).Ln(b.x) + C
remarque: toutes les intégrales sont définies à une constante C près appelée
constante d’intégration; la valeur de cette constante dépend des conditions initiales
au calcul d’aire; dans l’exemple précédent calculé avec Excel, on a initialisé le
calcul d’aire cumulée à zéro en écrivant dans la cellule “D2” la valeur 0; le calcul
ci-contre de la fonction intégrale y
2
= F(x) pour la valeur initiale (x = 0) donne
bien : y2 = -K.cos(0)+K = -K+K = 0
Bernard PONTALIER INITIATION PRATIQUE AU CALCUL INTÉGRAL p.3/4

Travaux pratiques:
Nous allons vérifier à l’aide du tableur-grapheur Excel le bien-fondé des formules
mathématiques.
• cas de la fonction afine: f(x) = a x + b
A B C D E
1
2
3
4
5
6
7
paramètres de calcul:
paramètres de calcul:
dx = 0,05 pas de calcul a = 0,5
Ao = 0 aire initiale b = 1
x f(x)=ax+b f(x) . dx aire cumulée F(x)
0 =ax+b =B6+dx =Ao =b*x+(a*x^2)/2
=A6+dx =ax+b =B7+dx =D6+C7 =b*x+(a*x^2)/2
on donne le nom “ dx ” à la cellule B2 , le nom “ Ao ” à la cellule B3 , le nom “a” à
la cellule E2 et le nom “ b ” à la cellule E3
F(x) = Intégrale de (a.x + b)
0
0,5
1
1,5
2
2,5
0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6
f(x)=ax+b
aire cumulée
F(x)
on remarque que les courbes de l’aire cumulée et de la fonction F(x), intégrale de
la fonction f(x), sont confondues
• cas de la fonction exponentielle: f(x) = e
a.x
A B C D E
1
2
3
4
5
6
7
paramètres de calcul:
paramètres de calcul:
dx = 0,05 pas de calcul a = 0,5
Ao = 0 aire initiale
x f(x)=exp(ax) f(x) . dx aire cumulée F(x)
0 =EXP(a*x) =B6+dx =Ao =(1/a)*EXP(a*x)
=A6+dx =EXP(a*x) =B7+dx =D6+C7 =(1/a)*EXP(a*x)
on donne le nom “ dx ” à la cellule B2 , le nom “ Ao ” à la cellule B3 et le nom “ a” à
la cellule E2
F(x) = Intégrale de Exponentielle (a.x)
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6
f(x)=exp(ax)
aire cumulée
F(x)
on remarque que les courbes de l’aire cumulée et de la fonction F(x), intégrale de
la fonction f(x), sont identiques mais décalées d’une quantité constante C égale à 2
dans cet exemple;
on retrouvera ces exemples dans le fichier Excel “TP calcul intégral.xls” ainsi que
ceux le la sinusoïde ou encore de l’hyperbole;
on constate à travers ces exemples que toutes les intégrales sont définies à une
constante C près appelée constante d’intégration.
Bernard PONTALIER INITIATION PRATIQUE AU CALCUL INTÉGRAL p.4/4