Concave et convexe

Concave et convexe
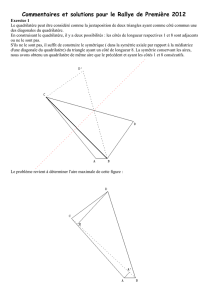
En feuilletant Problème ouvert et situation-problème de l'IREM, je suis tombé sur un problème (nu-
méro 44 page 87) qui m'a tout de suite intéressé. Il s'agissait de montrer que les triangles ABF et DEF
étaient congrus. En soi, il ne s'agit pas d'un problème trop difficile, probablement à la portée d'un élève de
deuxième secondaire.
R
15
B
20
-i- C
Vf
4 \
•V
-4
V V-
\ -
s S, ]
s
s Sj i, F
\ \ >
- V
s
- X s
t - S, V
1 12 ï 9 \
Il est possible de prouver l'égalité sans connaître la valeur de l'aire de chacun d'eux puisque l'aire de
chacun des triangles rectangles est de 210 et que les deux triangles rectangles ACD et BCE se partagent
une même région commune le quadrilatère convexe BCDF. Et si on voulait connaître la valeur de l'aire de
cette région commune...
Par Ghislain Desmeules
Séminaire de Métabetchouan
19

Quel est le rapport de l'aire du quadrilatère convexe BCDF et du quadrilatère concave ACEF ? En
d'autres mots, l'aire du premier représente quel pourcentage de l'aire du second ?
Puisque nous sommes en présence de triangles rectangles, il est possible d'utiliser la trigonométrie de
quatrième secondaire pour connaître la valeur des angles A, B, D et E.
Puisque tan A = on trouve A = 18,9246°.
Puièque tan 8 = on trouve B = 46,3972°.
Puisque tan D = "/12, on trouve D = 71,0754°.
Puisque tan E = on trouve E = 43,6028°.
Par soustraction, on trouve l'angle F = 27,4726°.
En utilisant la loi des sinus de cinquième secondaire, on trouve les mesures de BF et AF.
sin 18,9246° sin 27,4726° et sin 133,6028° sin 27,4726°
BF 15 AF 15
On trouve BF = 10,5454 On trouve AF = 23,5454
Nous connaissons maintenant la.longueur des trois côtés du triangle ABF et il est possible de connaître
l'aire d'un triangle en connaissant la longueur de ses côtés.
Il s'agit d'utiliser la formule de Héron d'Alexandri
A = V(s(s-AB){s-BF)(s-AF))
où s = 0,5 ( AB + BF + AF ) = 24,5454
Nous obtenons A = 57,2727 pour l'aire du triangle ABF.
L'aire du polygone convexe BCDF = 210 - 57,2727 = 152,7273.
L'aire du polygone concave ACEF = 210 + 57,2727 = 267,2727.
Le rapport des deux aires est de 4/7 et le pourcentage est de 571/7 %
D'une manière similaire, on peut trouver que DF = 13,4545 et aussi que FE = 18,4545. En utilisant à
nouveau la formule de Héron, on calcule bien entendu que l'aire du triangle DEF = 57,2727 aux arrondis
près.
Ma curiosité m'a tout de suite conduit à me poser la question : Qu'en est-il du rapport du périmètre du
polygone convexe BCDF à celui du polygone concave ACEF ? Le périmètre du premier représente quel
pourcentage du périmètre du second ?
20

Pour y parvenir la meilleure voie me semble être la géométrie analytique de quatrième secondaire puisque
nous connaissons les coordonnées des points A, B, D et E en considérant que le point C a comme coordon-
nées C(0,0).
Ainsi nous avons A(0,35) B(0,20) D(12,0) E(21,0)
Puisque mBE = l'équation de cette droite est 20x + 21y = 420.
Puisque mAD = -'yi2, l'équation de cette droite est 35x + 12y = 420.
En résolvant, on trouve les coordonnées du point FCVn, ""/n)
Pour trouver le périmètre du quadrilatère convexe BCDF, on doit faire la somme :
d(B,C) + d(C,D) + d(B,F) + d(D,F)
d(B,C) = 20
d(C,D) = 12
où d(B,F) = i (20 - + (0 - ) = V(80^ + 84^) = "«/n
et où d(D,F) = V( (0 - '"^/uf + (12 - ""/vf ) = + 48^) = '«/n
Nous trouvons ainsi 20 +12 + + '^/n = 56.
Pour trouver le périmètre du quadrilatère concave ACEF, on doit faire la somme :
d(A,C) + d(C,E) + d(A,F) + d(E,F)
d(A,C) = 35
d(C,E) = 21
où d(A,F) = V( (0 - + (35 - ) = V(842 + 245^) = '^Vv
et où d(E,F) = V( (21 - ""/uY + (0 - ) = ^(W +140^) = ^'«/i,
Nous trouvons ainsi 35 + 21 + + ^/v = 98.
Le rapport des périmètre est 56 -ï- 98 = ce qui est le même rapport que le rapport des aires de ces deux
quadrilatères.
En observant l'approche analytique, on s'aperçoit qu'elle aurait été suffisante pour trouver le rapport des
aires sans avoir à passer par la trigonométrie, la loi des sinus et la formule de Héron d'Alexandrie, comme me
l'a fait observé Simon, l'un de mes anciens élèves.
21

R( 0, 35)
B( 0, 20)
140/11
C( 0, 0)
\ \ 1
\ \
s
s s s >
"y \ c
s 's
\ s
! V S S
: \ s s
84/11 D( 12, 0) E(21,0)
Le problème ainsi envisagé peut être complètement résolu grâce à la géométrie analytique de qua-
trième secondaire. On pourrait montrer que l'aire du quadrilatère convexe BCDF est
140 X 84 + + 8yii + '^"/n X
11 11
1680
11
et celui du quadrilatère concave ACEF est
140 X 84 . ®yii X
11 11
2940
11
Les résultats obtenus m'ont quelque peu surpris, surtout lorsqu'on remarque que le rapport des aires
1680/,, ^294o/„ _ gt celui des périmètres 56 h-98 = "/? est le même, tout comme celui du prolongement des
côtés 12 H- 21 = "z? et 20 35 = "A. Je pensais que le rapport des aires serait égal au carré du rapport des
périmètres comme dans les figures semblables.
Il existe une foule de problèmes du même genre dont on peut maintenant prévoir le rapport des aires et
celui des périmètres.
22 envoi?f